
【题目】已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,对
,对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() .若正实数
.若正实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)详见解析;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)求导后,分别在![]() 和
和![]() 两种情况下根据导函数的正负求得函数的单调区间;
两种情况下根据导函数的正负求得函数的单调区间;
(2)通过分离变量得到![]() ,令
,令![]() ,利用导数可求得
,利用导数可求得![]() 最大值,由此得到
最大值,由此得到![]() ;
;
(3)设![]() ,以
,以![]() 为变量,令
为变量,令![]() ,通过判断导函数的正负可确定
,通过判断导函数的正负可确定![]() 在
在![]() 上单调递增,得到
上单调递增,得到![]() ,从而得到结论.
,从而得到结论.
(1)由题意知:![]() 定义域为
定义域为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,即
,即![]() 恒成立,
恒成立,
![]() 函数
函数![]() 的单调递增区间为
的单调递增区间为![]() ;无单调递减区间;
;无单调递减区间;
②当![]() 时,令
时,令![]() ,
,
解得:![]() ,
,![]() ,可知
,可知![]() ,
,
![]() 当
当![]() 和
和![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
![]() 的单调递增区间为
的单调递增区间为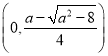 ,
,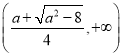 ;单调递减区间为
;单调递减区间为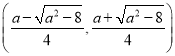 ;
;
综上所述:①当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
②当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为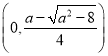 ,
,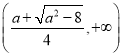 ,单调递减区间为
,单调递减区间为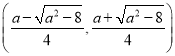 .
.
(2)![]() 对
对![]() 恒成立,即为对任意的
恒成立,即为对任意的![]() ,都有
,都有![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增;
单调递增;
当![]() ,
,![]() ,即
,即![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.
(3)证明:当![]() 时,
时,![]() ,
,
不妨设![]() ,以
,以![]() 为变量,令
为变量,令![]() ,
,
则![]()
![]() 且
且![]() ,
,
![]() ,即
,即![]() ,又
,又![]() 为增函数,
为增函数,
![]() ;
;
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
即![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,且
,且![]() ,
,![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() 为坐标原点,
为坐标原点,![]() 为定值,当
为定值,当![]() 变化时,始终有
变化时,始终有![]() ,求定值
,求定值![]() 的大小;
的大小;
(3)若![]() ,
,![]() ,
,![]() ,当
,当![]() 改变时,求三角形
改变时,求三角形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为![]() 内角A,B,C的对边,若
内角A,B,C的对边,若![]() 同时满足以下四个条件中的三个:①
同时满足以下四个条件中的三个:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
(1)条件①②能否同时满足,请说明理由;
(2)以上四个条件,请在满足三角形有解的所有组合中任选一组,并求出对应![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“众志成城,抗击疫情,一方有难,八方支援”,在此次抗击疫情过程中,各省市都派出援鄂医疗队. 假设汕头市选派![]() 名主任医生,
名主任医生,![]() 名护士,组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援,每个小组包括
名护士,组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援,每个小组包括![]() 名主任医生和
名主任医生和![]() 名护士,则不同的分配方案有( )
名护士,则不同的分配方案有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() 到直线
到直线![]() 的距离为10,圆
的距离为10,圆![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 为圆
为圆![]() 的任一直径,求
的任一直径,求![]() 的取值范围;
的取值范围;
(3)是否存在以椭圆上点![]() 为圆心的圆
为圆心的圆![]() ,使得过圆
,使得过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,都满足
,都满足![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】培养某种水生植物需要定期向培养植物的水中加入物质![]() ,已知向水中每投放1个单位的物质
,已知向水中每投放1个单位的物质![]() ,
,![]() (单位:天)时刻后水中含有物质
(单位:天)时刻后水中含有物质![]() 的量增加
的量增加![]() ,
,![]() 与
与![]() 的函数关系可近似地表示为关系可近似地表示为
的函数关系可近似地表示为关系可近似地表示为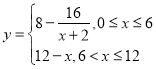 .根据经验,当水中含有物质
.根据经验,当水中含有物质![]() 的量不低
的量不低![]() 时,物质
时,物质![]() 才能有效发挥作用.
才能有效发挥作用.
(1)若在水中首次投放1个单位的物质![]() ,计算物质
,计算物质![]() 能持续有效发挥作用几天?
能持续有效发挥作用几天?
(2)若在水中首次投放1个单位的物质![]() ,第8天再投放1个单位的物质
,第8天再投放1个单位的物质![]() ,试判断第8天至第12天,水中所含物质
,试判断第8天至第12天,水中所含物质![]() 的量是否始终不超过
的量是否始终不超过![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com