练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】盒中有形状、大小都相同的2个红色球和3个黄色球，从中取出一个球，观察颜色后放回并往盒中加入同色球4个，再从盒中取出一个球，则此时取出黄色球的概率为（ ）

    A.B.C.D.

    【答案】A

    【解析】

    若取出的是红色球，再从盒中取出一个球，则此时取出黄色球的概率为：，若取出的是黄色球，再从盒中取出一个球，则此时取出黄色球的概率为：，由此能求出再从盒中取出一个球，则此时取出黄色球的概率.

    盒中有形状、大小都相同的2个红色球和3个黄色球，

    从中取出一个球，观察颜色后放回并往盒中加入同色球4个，

    若取出的是红色球，再从盒中取出一个球，

    则此时取出黄色球的概率为：，

    若取出的是黄色球，再从盒中取出一个球，

    则此时取出黄色球的概率为：，

    ∴再从盒中取出一个球，则此时取出黄色球的概率为：，

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】作家马伯庸小说《长安十二时辰》中，靖安司通过长安城内的望楼传递信息.同名改编电视剧中，望楼传递信息的方式有一种如下：如图所示，在九宫格中，每个小方格可以在白色和紫色（此处以阴影代表紫色）之间变换，从而一共可以有512种不同的颜色组合，即代表512种不同的信息.现要求每一行，每一列上至多有一个紫色小方格（如图所示即满足要求）.则一共可以传递______种信息.（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中国，“女排精神”概括的是顽强战斗、勇敢拼搏精神.在某年度排球超级杯决赛中，中国女排与俄罗斯女排相遇，已知前四局中，战成了，且在决胜局中，中国队与俄罗斯队战成了，根据中国队与俄罗斯队以往的较量，每个球中国队获胜的概率为，假定每个球中国队是否获胜相互独立，则再打不超过4球，中国队获得比赛胜利的概率为（ ）

    （注：排球的比赛规则为5局3胜制，即比赛双方中的一方先拿到3局胜利为获胜队，其中前四局为25分制，即在一方先得到25分，且与对方的分差大于或等于2分，则先拿到25分的一方胜；若一方拿到25分后，但双方分差小于2分，则比赛继续，直到一方领先2分为止；若前四局打成，则决胜局采用15分制.）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，圆的参数方程为（为参数），直线的参数方程为（为参数），设原点在圆的内部，直线与圆交于、两点；以坐标原点为极点，轴的正半轴为极轴建立极坐标系.

    （1）求直线和圆的极坐标方程，并求的取值范围；

    （2）求证：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在极坐系中，点绕极点顺时针旋转角得到点.以为原点，极轴为轴非负半轴，并取相同的单位长度建立平面直角坐标系，曲线：绕逆时针旋转得到曲线.

    （1）求曲线的极坐标方程和曲线的直角坐标方程；

    （2）点的极坐标为，直线过点且与曲线交于，两点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量x（）（件）与相应的生产总成本y（万元）的四组对照数据.

    x

    5

    7

    9

    11

    y

    200

    298

    431

    609

    工厂研究人员建立了y与x的两种回归模型,利用计算机算得近似结果如下：

    模型①：

    模型②：.

    其中模型①的残差（实际值－预报值）图如图所示：

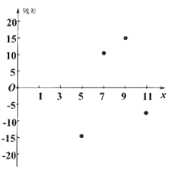
    （1）根据残差分析,判断哪一个模型更适宜作为y关于x的回归方程？并说明理由；

    （2）市场前景风云变幻,研究人员统计历年的销售数据得到每件产品的销售价格q（万元）是一个与产量x相关的随机变量,分布列为：

    q

    P

    0.5

    0.4

    0.1

    结合你对（1）的判断,当产量x为何值时,月利润的预报期望值最大？最大值是多少（精确到0.1）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，、、两两垂直，，，，为线段上一点（端点除外）.

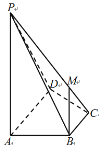
    （1）若异面直线、所成角的余弦值为，求的长；

    （2）求二面角的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（0＜b＜2）的离心率为，F为椭圆的右焦点，PQ为过中心O的弦．

    （1）求面积的最大值；

    （2）动直线与椭圆交于A，B两点，证明：在第一象限内存在定点M，使得当直线AM与直线BM的斜率均存在时，其斜率之和是与t无关的常数，并求出所有满足条件的定点M的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱柱中，平面ABCD，底面ABCD是矩形，，，，M为的中点．

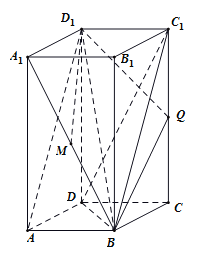
    （1）求证：D1M//平面BDC1；

    （2）若棱上存在点Q，满足与平面所成角的正弦值为，求异面直线与BQ所成角的余弦值．

    查看答案和解析>>

    同步练习册答案