
【题目】已知平面向量![]() ,
,![]() ,
,![]() 满足:
满足:![]() ,
,![]() 的夹角为
的夹角为![]() ,|
,|![]() |=5,
|=5,![]() ,
,![]() 的夹角为
的夹角为![]() ,|
,|![]() |=3
|=3![]() ,则
,则![]()
![]() 的最大值为_____.
的最大值为_____.
【答案】36
【解析】
设![]() ,
,![]() ,
,![]() ,由题意知
,由题意知![]() 四点共圆,建立坐标系,求出点
四点共圆,建立坐标系,求出点![]() 的坐标和圆的半径,设
的坐标和圆的半径,设![]() ,用
,用![]() 表示
表示![]() ,根据
,根据![]() 范围和三角和差公式,即可求解.
范围和三角和差公式,即可求解.
设![]() ,
,![]() ,
,![]() ,
,
则AB=|![]() |=5,AC=|
|=5,AC=|![]() |=3
|=3![]() ,∠ACB
,∠ACB![]() ,∠APB
,∠APB![]() ,
,
可得P,A,B,C四点共圆.
设△ABC的外接圆的圆心为O,则∠AOB=2∠APB![]() ,
,
由正弦定理可知:2OA![]() 5
5![]() ,故OA
,故OA![]() .
.
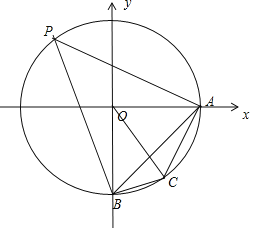
以O为圆心,以OA,OB为坐标轴建立平面坐标系如图所示:
则A(![]() ,0),B(0,
,0),B(0,![]() ).
).
在△OAC中,由余弦定理可得cos∠AOC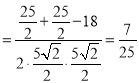 ,
,
故sin∠AOC![]() ,∴C(
,∴C(![]() ,
,![]() ).
).
设P(![]() cosα,
cosα,![]() sinα),
sinα),![]() ,
,
则![]() (
(![]() cosα,
cosα,![]() sinα),
sinα),![]() (
(![]() cosα,
cosα,![]() sinα),
sinα),
∴![]() (
(![]() cosα)(
cosα)(![]() cosα)
cosα)![]() sinα(
sinα(![]() sinα)
sinα)
=16+12sinα﹣16cosα=16+20(![]() sinα
sinα![]() cosα)
cosα)
=16+20sin(α﹣φ),其中sinφ![]() ,cosφ
,cosφ![]() .
.
∴当α=φ![]() 时,
时,![]() 取得最大值36.
取得最大值36.
答案:36.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线Γ的准线方程为![]() .焦点为
.焦点为![]() .
.
(1)求证:抛物线Γ上任意一点![]() 的坐标
的坐标![]() 都满足方程:
都满足方程:![]()
(2)请求出抛物线Γ的对称性和范围,并运用以上方程证明你的结论;
(3)设垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(ax+b)﹣x(a,b∈R,ab≠0).
(1)讨论f(x)的单调性;
(2)若f(x)≤0恒成立,求ea(b﹣1)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com