
| OB |
| OA |
| OC |
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| 3 |
| n |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
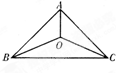 三个城市襄阳、荆州、武汉分别位于A,B,C三点处(如右图),且AB=AC=20
三个城市襄阳、荆州、武汉分别位于A,B,C三点处(如右图),且AB=AC=20| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州中学高三(上)第一次质量检测数学试卷 (理科)(解析版) 题型:解答题
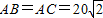 km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.
km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.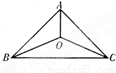
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com