
【题目】已知数列{an}中,a1=2,an+1﹣an﹣2n﹣2=0(n∈N*).
(1)求数列{an}的通项公式;
(2)设 ![]() ,若对任意的正整数n,当m∈[﹣1,1]时,不等式
,若对任意的正整数n,当m∈[﹣1,1]时,不等式 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
【答案】
(1)解:由题意得an+1﹣an﹣2n﹣2=0,则an+1﹣an=2n+2,
∴an﹣an﹣1=2n(n≥2),
∴a2﹣a1=2×2,a3﹣a2=2×3,…,an﹣an﹣1=2n,
通过叠加得an=2(2+3+…+n)+a1
=2× ![]() +2=n(n+1)(n≥2).
+2=n(n+1)(n≥2).
又∵a1=2符合此通项公式,
∴an=n(n+1)
(2)解:由(1)得, ![]()
= ![]() +…+
+…+ ![]()
=( ![]() )+(
)+( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )
)
= ![]() =
= ![]() =
= ![]() ,
,
设y=2x+ ![]() +3,则函数在(
+3,则函数在( ![]() ,+∞)上递增,
,+∞)上递增,
∴当n=1时, ![]() 取到最小值为6,
取到最小值为6,
∴bn的最大值为 ![]() ,
,
故要使不等式 ![]() 对一切m∈[﹣1,1]成立,
对一切m∈[﹣1,1]成立,
须使 ![]() ,即t2﹣2mt>0对一切m∈[﹣1,1]恒成立.
,即t2﹣2mt>0对一切m∈[﹣1,1]恒成立.
设g(m)=t2﹣2mt,
当t=0时,g(m)>0不成立,
当t≠0时,g(m)是一次函数,
则 ![]() ,即
,即 ![]() ,解得t>2或t<﹣2,
,解得t>2或t<﹣2,
综上得,t的取值范围是(﹣∞,﹣2)∪(2,+∞)
【解析】(1)由题意得an﹣an﹣1=2n(n≥2),再给n具体值列出方程,利用叠加法和等差数列的前n项和公式,求出an;(2)由(1)表示出bn , 再通过裂项相消法化简bn , 构造函数y=2x+ ![]() +3判断出单调性,再求出
+3判断出单调性,再求出 ![]() 的最小值,即求出bn的最大值,由恒成立列出不等式:t2﹣2mt>0,再一次构造函数g(m)=t2﹣2mt,并进行分类列出恒成立的条件,求出t的范围.
的最小值,即求出bn的最大值,由恒成立列出不等式:t2﹣2mt>0,再一次构造函数g(m)=t2﹣2mt,并进行分类列出恒成立的条件,求出t的范围.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系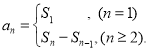 .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且当x=
)的最小正周期是π,且当x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式(a2﹣a)4x﹣2x﹣1<0在区间(﹣∞,1]上恒成立,则实数a的取值范围为( )
A.(﹣2, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,6]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() =80,
=80, ![]() =20,
=20, ![]() iyi=184,
iyi=184, ![]()
![]() =720.(b=
=720.(b= 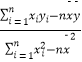 )
)
(1)求家庭的月储蓄y对月收入x的线性回归方程;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①三点确定一个平面;
②三条两两相交的直线确定一个平面;
③在空间上,与不共面四点A,B,C,D距离相等的平面恰有7个;
④两个相交平面把空间分成四个区域.
其中真命题的序号是 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
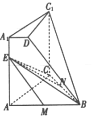
【题目】如图,几何体![]() 由一个正三棱柱截去一个三棱锥而得,
由一个正三棱柱截去一个三棱锥而得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
(1)若![]() 在棱
在棱![]() 上,且
上,且![]() ,证明:
,证明: ![]() 平面
平面![]() ;
;
(2)过![]() 作平面
作平面![]() 的垂线,垂足为
的垂线,垂足为![]() ,确定
,确定![]() 的位置(说明作法及理由),并求线段
的位置(说明作法及理由),并求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的环保意识,某市面向全市增招环保知识义务宣传志愿者,从符合条件的志愿者中随机选取![]() 名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第
名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图(局部)如图所示.
,得到的频率分布直方图(局部)如图所示.
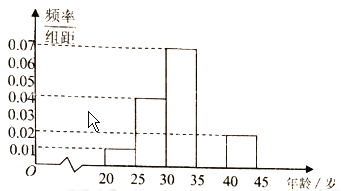
(1)求第![]() 组的频率,并在图中补画直方图;
组的频率,并在图中补画直方图;
(2)从![]() 名志愿者中再选出年龄低于
名志愿者中再选出年龄低于![]() 岁的志愿者
岁的志愿者![]() 名担任主要宣讲人,求这
名担任主要宣讲人,求这![]() 名主要宣讲人的年龄在不同一组的概率.
名主要宣讲人的年龄在不同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com