
【题目】如果存在常数k使得无穷数列![]() 满足
满足![]() 恒成立,则称为
恒成立,则称为![]() 数列.
数列.
(1)若数列![]() 是
是![]() 数列,
数列,![]() ,
,![]() ,求
,求![]() ;
;
(2)若等差数列![]() 是
是![]() 数列,求数列
数列,求数列![]() 的通项公式;
的通项公式;
(3)是否存在![]() 数列
数列![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,…是等比数列?若存在,请求出所有满足条件的数列
,…是等比数列?若存在,请求出所有满足条件的数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)存在;满足条件的
;(3)存在;满足条件的![]() 数列
数列![]() 有无穷多个,其通项公式为
有无穷多个,其通项公式为![]() .
.
【解析】
(1)根据![]() 数列的定义,得
数列的定义,得![]() ,
,![]() ,可求
,可求![]() ;
;
(2)根据![]() 数列的定义,得
数列的定义,得![]() ,分
,分![]() 和
和![]() 两种情况讨论. 当
两种情况讨论. 当![]() ,
,![]() .当
.当![]() 时,由
时,由![]() 是等差数列,对
是等差数列,对![]() 赋值,求出
赋值,求出![]() 和公差
和公差![]() ,即求
,即求![]() ;
;
(3)假设存在满足条件的![]() 数列
数列![]() ,设等比数列
,设等比数列![]() ,
,![]() ,
,![]() ,…的公比为q.则有
,…的公比为q.则有![]() ,
,![]() ,可得q=1,故当
,可得q=1,故当![]() 时,
时,![]() .当
.当![]() 时,不妨设
时,不妨设![]() ,
,![]() 且i为奇数,
且i为奇数,
由![]() ,可得
,可得![]() .
.
即满足条件的![]() 数列
数列![]() 有无穷多个,其通项公式为
有无穷多个,其通项公式为![]() .
.
(1)由数列![]() 是
是![]() 数列,得
数列,得![]() ,
,![]() ,可得
,可得![]() ;
;
(2)由![]() 是
是![]() 数列知
数列知![]() 恒成立,取m=1得
恒成立,取m=1得![]() 恒成立,
恒成立,
当![]() ,
,![]() 时满足题意,此时
时满足题意,此时![]() ,
,
当![]() 时,由
时,由![]() 可得
可得![]() ,取m=n=2得
,取m=n=2得![]() ,
,
设公差为d,则![]() 解得
解得![]() 或者
或者![]() ,
,
综上,![]() 或
或![]() 或
或![]() ,经检验均合题意.
,经检验均合题意.
(3)假设存在满足条件的![]() 数列
数列![]() ,
,
不妨设该等比数列![]() ,
,![]() ,
,![]() ,…的公比为q,
,…的公比为q,
则有![]() ,
,
可得![]() ①
①
![]() ,
,
可得![]() ②
②
综上①②可得q=1,
故![]() ,代入
,代入![]() 得
得![]() ,
,
则当![]() 时,
时,![]() ,
,
又![]() ,
,
当![]() 时,不妨设
时,不妨设![]() ,
,![]() 且i为奇数,
且i为奇数,
由![]() ,
,
而![]() ,
,![]() ,
,![]() ,
,![]() .
.
综上,满足条件的![]() 数列
数列![]() 有无穷多个,其通项公式为
有无穷多个,其通项公式为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】超级细菌是一种耐药性细菌,产生超级细菌的主要原因是用于抵抗细菌侵蚀的药物越来越多,但是由于滥用抗生素的现象不断的发生,很多致病菌也对相应的抗生素产生了耐药性,更可怕的是,抗生素药物对它起不到什么作用,病人会因为感染而引起可怕的炎症,高烧,痉挛,昏迷甚至死亡.某药物研究所为筛查某种超级细菌,需要检验血液是否为阳性,现有n(![]() )份血液样本,每个样本取到的可能性相等,有以下两种检验方式:(1)逐份检验,则需要检验n次;(2)混合检验,将其中k(
)份血液样本,每个样本取到的可能性相等,有以下两种检验方式:(1)逐份检验,则需要检验n次;(2)混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,则这份的血液全为阴性,因而这k份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为
)份血液样本分别取样混合在一起检验,若检验结果为阴性,则这份的血液全为阴性,因而这k份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).现取其中k(
).现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)运用概率统计的知识,若![]() ,试求P关于k的函数关系式
,试求P关于k的函数关系式![]() ;
;
(2)若P与抗生素计量![]() 相关,其中
相关,其中![]() ,
,![]() ,…,
,…,![]() (
(![]() )是不同的正实数,满足
)是不同的正实数,满足![]() ,对任意的
,对任意的![]() (
(![]() ),都有
),都有![]() .
.
(i)证明:![]() 为等比数列;
为等比数列;
(ii)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数期望值比逐份检验的总次数期望值更少,求k的最大值.
时,采用混合检验方式可以使得样本需要检验的总次数期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
![]() 若
若![]() ,
,![]() ,①若函数
,①若函数![]() 单调递增,求实数
单调递增,求实数![]() 的取值范围;②若对任意
的取值范围;②若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
![]() 若
若![]() ,且
,且![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是平面![]() 的斜线段,A为斜足,点C满足
的斜线段,A为斜足,点C满足![]() ,且在平面
,且在平面![]() 内运动,则有以下几个命题:
内运动,则有以下几个命题:

①当![]() 时,点C的轨迹是抛物线;
时,点C的轨迹是抛物线;
②当![]() 时,点C的轨迹是一条直线;
时,点C的轨迹是一条直线;
③当![]() 时,点C的轨迹是圆;
时,点C的轨迹是圆;
④当![]() 时,点C的轨迹是椭圆;
时,点C的轨迹是椭圆;
⑤当![]() 时,点C的轨迹是双曲线.
时,点C的轨迹是双曲线.
其中正确的命题是__________.(将所有正确的命题序号填到横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在
时,是否存在![]() ,使得不等式
,使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的快速增长、规模的迅速扩张以及人民生活水平的逐渐提高,日益剧增的垃圾给城市的绿色发展带来了巨大的压力.相关部门在有5万居民的光明社区采用分层抽样方法得到年内家庭人均![]() 与人均垃圾清运量的统计数据如下表:
与人均垃圾清运量的统计数据如下表:
人均 | 3 | 6 | 9 | 12 | 15 |
人均垃圾清运量 | 0.13 | 0.23 | 0.31 | 0.41 | 0.52 |
(1)已知变量![]() 与
与![]() 之间存在线性相关关系,求出其回归直线方程;
之间存在线性相关关系,求出其回归直线方程;
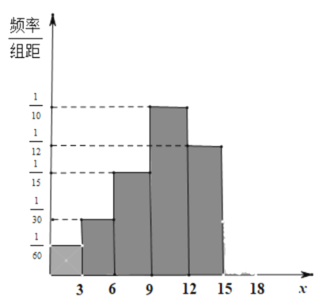
(2)随着垃圾分类的推进,燃烧垃圾发电的热值大幅上升,平均每吨垃圾可折算成上网电量200千瓦时,如图是光明社区年内家庭人均![]() 的频率分布直方图,请补全
的频率分布直方图,请补全![]() 的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网电量.
的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网电量.
参考公式]回归方程![]() ,
,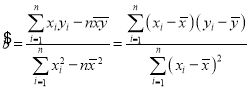
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】植物园拟建一个多边形苗圃,苗圃的一边紧靠着长度大于30m的围墙.现有两种方案:
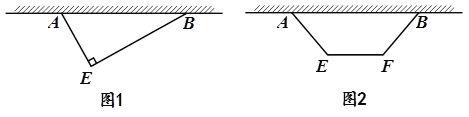
方案① 多边形为直角三角形![]() (
(![]() ),如图1所示,其中
),如图1所示,其中![]() ;
;
方案② 多边形为等腰梯形![]() (
(![]() ),如图2所示,其中
),如图2所示,其中![]() .
.
请你分别求出两种方案中苗圃的最大面积,并从中确定使苗圃面积最大的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com