
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求
,求![]() 的面积最大值.
的面积最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题(1)将曲线![]() 的参数方程和直线
的参数方程和直线![]() 的极坐标方程化为普通方程,然后利用圆心到直线的距离为半径建立等量关系,求解参数
的极坐标方程化为普通方程,然后利用圆心到直线的距离为半径建立等量关系,求解参数![]() 的值;(2)借助极坐标方程中极角的几何意义和三角变换,将
的值;(2)借助极坐标方程中极角的几何意义和三角变换,将![]() 的面积公式转化为含有一个角的一个三角函数,利用三角函数的图象探求最值问题.
的面积公式转化为含有一个角的一个三角函数,利用三角函数的图象探求最值问题.
(Ⅰ)曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆;
为半径的圆;
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由直线![]() 与圆
与圆![]() 只有一个公共点,则可得
只有一个公共点,则可得![]() ,
,
解得: ![]() (舍),
(舍),![]() .
.
所以:![]()
(Ⅱ)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
设![]() 的极角为
的极角为![]() ,
, ![]() 的极角为
的极角为![]() ,
,
则![]() ,
,
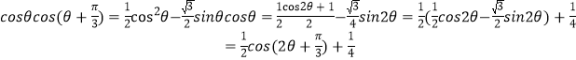 所以当
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
![]() 的面积最大值
的面积最大值![]() .
.
解法二:因为曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,且
为半径的圆,且![]()
由正弦定理得:![]() ,所以
,所以![]() .
.
由余弦定理得![]() ,
,
所以![]() ,
,
所以![]() 的面积最大值
的面积最大值![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,已知PA⊥平面ABCD,△ABC为等边三角形,PA=2AB=2,AC⊥CD,PD与平面PAC所成角的余弦值为![]() .
.
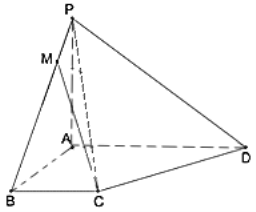
(1)证明:![]() 平面PAD;
平面PAD;
(2)点M为PB上一点,且![]() ,试判断点M的位置.
,试判断点M的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点
为极点![]() ,轴的正半轴为极轴建立极坐标系,圆
,轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)直线![]() 与圆
与圆![]() 相交于不同两点
相交于不同两点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹的参数方程.
的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月23日中国人民海军建军70周年.为展现人民海军70年来的辉煌历程和取得的巨大成就,我国在山东青岛及附近海空举行盛大的阅兵仪式.我国第一艘航空母舰“辽宁舰”作战群将参加军演,要求2艘攻击型核潜艇一前一后,3艘驱逐舰和3艘护卫舰分列左右,每侧3艘,同侧不能都是同种舰艇,则舰艇分配方案的方法种数为( )
A.1296B.648C.324D.72
查看答案和解析>>
科目:高中数学 来源: 题型:
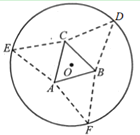
【题目】如图,要利用一半径为![]() 的圆形纸片制作三棱锥形包装盒.已知该纸片的圆心为
的圆形纸片制作三棱锥形包装盒.已知该纸片的圆心为![]() ,先以
,先以![]() 为中心作边长为
为中心作边长为![]() (单位:
(单位:![]() )的等边三角形
)的等边三角形![]() ,再分别在圆
,再分别在圆![]() 上取三个点
上取三个点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合于点
重合于点![]() ,即可得到正三棱锥
,即可得到正三棱锥![]() .
.

(1)若三棱锥![]() 是正四面体,求
是正四面体,求![]() 的值;
的值;
(2)求三棱锥![]() 的体积
的体积![]() 的最大值,并指出相应
的最大值,并指出相应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了加强对“新型冠状病毒”的防控,确保居民在小区封闭期间生活不受影响,小区超市采取有力措施保障居民正常生活物资供应.为做好甲类生活物资的供应,超市对社区居民户每天对甲类生活物资的购买量进行了调查,得到了以下频率分布直方图.
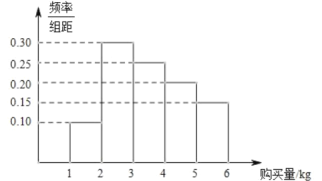
(1)从小区超市某天购买甲类生活物资的居民户中任意选取5户.
①若将频率视为概率,求至少有两户购买量在![]() (单位:
(单位:![]() )的概率是多少?
)的概率是多少?
②若抽取的5户中购买量在![]() (单位:
(单位:![]() )的户数为2户,从5户中选出3户进行生活情况调查,记3户中需求量在
)的户数为2户,从5户中选出3户进行生活情况调查,记3户中需求量在![]() (单位:
(单位:![]() )的户数为
)的户数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)将某户某天购买甲类生活物资的量与平均购买量比较,当超出平均购买量不少于![]() 时,则称该居民户称为“迫切需求户”,若从小区随机抽取10户,且抽到k户为“迫切需求户”的可能性最大,试求k的值.
时,则称该居民户称为“迫切需求户”,若从小区随机抽取10户,且抽到k户为“迫切需求户”的可能性最大,试求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
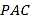
图一
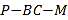
图二
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com