
【题目】已知抛物线C: ![]() ,点
,点![]() .
.
(1)求点P与抛物线C的焦点F的距离;
(2)设斜率为l的直线l与抛物线C交于A,B两点若△PAB的面积为![]() ,求直线l的方程;
,求直线l的方程;
(3)是否存在定圆M: ![]() ,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)P(1,0),距离为5;(2)y=x﹣1;(3)Q,存在实数m=3,使得直线AB与圆M相切.
【解析】
(1)求得抛物线的焦点坐标,由两点距离公式,计算可得所求距离;
(2)设直线l的方程为y=x+a,代入抛物线的方程,运用韦达定理和弦长公式以及三角形的面积公式,解方程可得a,进而得到直线方程;
(3)取Q(0,0),切线为y=kx,求得切点A,B,和直线AB,由相切可得m=3,证明对任意的动点Q,直线AB与圆相切,必有m=3.设Q(![]() a2,a),l:x=t(y﹣a)
a2,a),l:x=t(y﹣a)![]() a2,A(
a2,A(![]() y12,y1),B(
y12,y1),B(![]() y22,y2),运用直线和圆相切的条件和韦达定理,求得AB的方程,计算圆心到直线AB的距离,即可得证.
y22,y2),运用直线和圆相切的条件和韦达定理,求得AB的方程,计算圆心到直线AB的距离,即可得证.
(1)抛物线C:y2=4x的焦点坐标为(1,0),
则点P与抛物线C的焦点F的距离为![]() 5;
5;
(2)设直线l的方程为y=x+a,
把y=x+a方程代入抛物线y2=4x,
可得x2+2(a﹣2)x+a2=0,
∴x1+x2=4﹣2a,x1x2=a2,
∴|AB|![]() |x1﹣x2|
|x1﹣x2|
![]() 4
4![]() ,
,
点P到直线的距离d![]() ,
,
∴S△PAB![]() |AB|d
|AB|d
![]() 4
4![]() 2
2![]() ,
,
解得a=﹣1,
∴直线l的方程y=x﹣1;
(3)取Q(0,0),圆(x﹣m)2+y2=4,切线为y=kx,
由![]() 2,解得k2
2,解得k2![]() ,①
,①
将直线y=kx代入抛物线方程y2=4x,
解得A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
直线AB的方程为x![]() ,
,
若直线和圆相切,可得|![]() m|=2②
m|=2②
由①②解得m=3或2(舍去).
综上可得,对任意的动点Q,直线AB与圆相切,必有m=3.
下证m=3时,对任意的动点Q,直线AB和圆相切.
理由如下:设Q(![]() a2,a),l:x=t(y﹣a)
a2,a),l:x=t(y﹣a)![]() a2,A(
a2,A(![]() y12,y1),B(
y12,y1),B(![]() y22,y2),
y22,y2),
由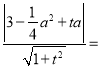 2,可得(a2﹣4)t2﹣(
2,可得(a2﹣4)t2﹣(![]() a2﹣6)at+(
a2﹣6)at+(![]() a2﹣3)2﹣4=0,
a2﹣3)2﹣4=0,
∴t1+t2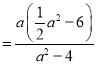 ,t1t2
,t1t2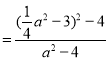 ,
,
又直线与曲线相交于A,B,
由x=t(y﹣a)![]() a2,代入抛物线方程可得y2﹣4ty+4ta﹣a2=0,
a2,代入抛物线方程可得y2﹣4ty+4ta﹣a2=0,
可得y12=4t1(y1﹣a)+a2,y22=4t2(y2﹣a)+a2,
则a,y1是方程y2=4t1(y﹣a)+a2的两根,
即有ay1=4t1a﹣a2,即为y1=4t1﹣a,同理y2=4t2﹣a.
则有A(![]() (4t1﹣a)2,4t1﹣a),B(
(4t1﹣a)2,4t1﹣a),B(![]() (4t2﹣a)2,4t2﹣a),
(4t2﹣a)2,4t2﹣a),
直线AB:y﹣(4t1﹣a)![]() (x
(x![]() (4t1﹣a)2),
(4t1﹣a)2),
即为y﹣(4t1﹣a)![]() (x
(x![]() (4t1﹣a)2),
(4t1﹣a)2),
则圆心(3,0)到直线AB的距离为
d ,
,
由(a2﹣4)t12﹣(![]() a2﹣6)at1+(
a2﹣6)at1+(![]() a2﹣3)2﹣4=0,
a2﹣3)2﹣4=0,
代入上式,化简可得d![]() 2,
2,
则有对任意的动点Q,存在实数m=3,使得直线AB与圆M相切.
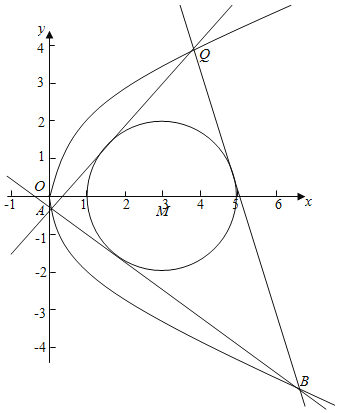


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() :
:![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动,![]() 是线段
是线段![]() 与
与![]() 轴的交点,动点
轴的交点,动点![]() 满足:
满足:![]() ,
,![]() .
.
(1)求动点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线与曲线
的垂线与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一个长轴顶点在直线
,一个长轴顶点在直线![]() 上,若直线
上,若直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求该椭圆的方程.
(2)若![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中系列的幅面规格为:①
系列,其中系列的幅面规格为:①![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所有规格的纸张的幅宽(以
所有规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系都为
表示)的比例关系都为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 纸各一张.若
纸各一张.若![]() 纸的宽度为
纸的宽度为![]() ,则
,则![]() 纸的面积为________
纸的面积为________![]() ;这
;这![]() 张纸的面积之和等于________
张纸的面积之和等于________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .(
.(![]() 是常数,且(
是常数,且(![]() )
)
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求证:当![]() 时
时![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班上午有五节课,分別安排语文,数学,英语,物理,化学各一节课.要求语文与化学相邻,数学与物理不相邻,且数学课不排第一节,则不同排课法的种数是
A. 24B. 16C. 8D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com