
【题目】设偶函数![]() 和奇函数
和奇函数![]() 的图象如图所示,集合A
的图象如图所示,集合A ![]() 与集合B
与集合B ![]() 的元素个数分别为a,b,若
的元素个数分别为a,b,若![]() ,则a+b的值不可能是( )
,则a+b的值不可能是( )

A. 12B. 13C. 14D. 15
【答案】D
【解析】
利用f(x),g(x)图象,分别判断g(x)=t和f(x)=t,在![]() <t<1时的取值情况,进行分类讨论即可.
<t<1时的取值情况,进行分类讨论即可.
由条件知,第一个图象为f(x)的图象,第二个为g(x)的图象.
由图象可知若f(x)=0,则x有3个解,为x=﹣![]() ,x=0,x=
,x=0,x=![]() ,若g(x)=0,则x有3个解,不妨设为x=-n,x=0,x=n,(0<n<1)
,若g(x)=0,则x有3个解,不妨设为x=-n,x=0,x=n,(0<n<1)
当f(g(x)﹣t)=0得g(x)﹣t=![]() ,或g(x)﹣t=0,或g(x)﹣t=﹣
,或g(x)﹣t=0,或g(x)﹣t=﹣![]() ,.
,.
即g(x)=t+![]() ,或g(x)=t,或g(x)=t﹣
,或g(x)=t,或g(x)=t﹣![]() .
.![]()
![]() <t<1时,
<t<1时,
若g(x)=t,得x有3个解;
若g(x)=t﹣![]()
![]() ,此时x有3个解;
,此时x有3个解;
若g(x)=t+![]()
![]() ,此时方程无解.所以a=3+3=6.
,此时方程无解.所以a=3+3=6.
当g(f(x)﹣t)=0得f(x)﹣t=n,或f(x)﹣t=0或f(x)﹣t=﹣n.
即f(x)=t+n,或f(x)=t,或f(x)=t﹣n.![]()
![]() <t<1,0<n<1,
<t<1,0<n<1,
若f(x)=t,所以此时x有4个解.
若f(x)=t+n,当0<n<![]() ,则
,则![]() <t+n<
<t+n<![]() ,此时x有4个解或2解或0个解.对应f(x)=t﹣n∈(0,1)有4个解,
,此时x有4个解或2解或0个解.对应f(x)=t﹣n∈(0,1)有4个解,
此时b=4+4+4=12或b=4+2+4=10或b=4+0+4=8.
若![]() ,则1<t+n<2,此时x无解.对应f(x)=t﹣n∈(
,则1<t+n<2,此时x无解.对应f(x)=t﹣n∈(![]() ,
,![]() )有2个解或3解或4个解.
)有2个解或3解或4个解.
所以此时b=4+2=6或b=4+3=7或b=4+4=8.
综上b=12或10或8或6或7.所以a+b=18或16或14或13或12.
故选:D.


科目:高中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,现计划在两地间以
,现计划在两地间以![]() 为端点的线段上,选择一点
为端点的线段上,选择一点![]() 处建造畜牧养殖场,其对两地的影响度与所选地点到两地的距离有关,对
处建造畜牧养殖场,其对两地的影响度与所选地点到两地的距离有关,对![]() 地和
地和![]() 地的总影响度为对地和地的影响度之和,记点
地的总影响度为对地和地的影响度之和,记点![]() 到
到![]() 地的距离为
地的距离为![]() ,建在
,建在![]() 处的畜牧养殖场对
处的畜牧养殖场对![]() 地和
地和![]() 地的总影响度为
地的总影响度为![]() .统计调查表明:畜牧养殖场对
.统计调查表明:畜牧养殖场对![]() 地的影响度与所选地点到
地的影响度与所选地点到![]() 地的距离成反比,比例系数为
地的距离成反比,比例系数为![]() ;对
;对![]() 地的影响度与所选地点到
地的影响度与所选地点到![]() 地的距离成反比,比例系数为
地的距离成反比,比例系数为![]() ,当畜牧养殖场建在线段
,当畜牧养殖场建在线段![]() 中点处时,对
中点处时,对![]() 地和
地和![]() 地的总影响度为
地的总影响度为![]() .
.
(1)将![]() 表示为
表示为![]() 的函数,写出函数的定义域;
的函数,写出函数的定义域;
(2)当点![]() 到地
到地![]() 的距离为多少时,建在此处的畜牧养殖场对
的距离为多少时,建在此处的畜牧养殖场对![]() 地和
地和![]() 地的总影响度最小?并求出总影响度的最小值.
地的总影响度最小?并求出总影响度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,四边形
中,四边形![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 上的动点.
上的动点.
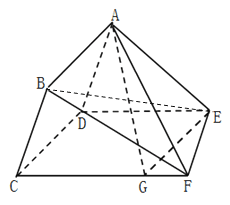
(Ⅰ)当![]() 时,求证
时,求证![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若二面角![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com