
【题目】已知函数 ![]() ,
, ![]() .
.
(I)求 ![]() 的单调区间;
的单调区间;
(II)若对任意的 ![]() ,都有
,都有 ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:(I) ![]() , 当
, 当 ![]() 时,
时, ![]() 恒成立,则
恒成立,则 ![]() 在
在 ![]() 上单调递增;当
上单调递增;当 ![]() 时,令
时,令 ![]() ,则
,则 ![]() .则
.则 ![]() 在区间
在区间 ![]() 上单调递增,在区间
上单调递增,在区间 ![]() 上单调递减.
上单调递减.
(II) ![]() ,
, ![]() 等价于
等价于 ![]() .令
.令 ![]() ,则
,则 ![]() .
.
令 ![]() ,则
,则 ![]() .
.
因为当 ![]() ,
, ![]() 恒成立,
恒成立,
所以 ![]() 在
在 ![]() 上单调递减.
上单调递减.
又 ![]() ,可得
,可得 ![]() 和
和 ![]() 在
在 ![]() 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| 单调递增 | 单调递减 |
所以 ![]() 在
在 ![]() 上的最大值为
上的最大值为 ![]() .
.
因此 ![]() ,
, ![]() 等价于
等价于 ![]() .
.
故 ![]() ,
, ![]() 时,实数
时,实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】(1)根据题意求出导函数利用导函数的性质即可得到原函数的单调性。(2)根据题意 x ∈ ( 0 , + ∞ ) , f ( x ) ≤ 2 a 2 等价![]() ,构造函数 g ( x ),对其求导利用导函数的性质能求出 x ∈ ( 0 , + ∞ ) , f ( x ) ≤ 2 a 2 时,即可求出a的取值范围。
,构造函数 g ( x ),对其求导利用导函数的性质能求出 x ∈ ( 0 , + ∞ ) , f ( x ) ≤ 2 a 2 时,即可求出a的取值范围。
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
【题目】已知各项不为零的数列{an}的前n项和为Sn , 且a1=1,Sn=panan+1(n∈N*),p∈R.
(1)若a1 , a2 , a3成等比数列,求实数p的值;
(2)若a1 , a2 , a3成等差数列,
①求数列{an}的通项公式;
②在an与an+1间插入n个正数,共同组成公比为qn的等比数列,若不等式(qn)(n+1)(n+a)≤e对任意的n∈N*恒成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分),以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界线符合函数y=x+ ![]() (x>0)模型,园区服务中心P在x轴正半轴上,PO=
(x>0)模型,园区服务中心P在x轴正半轴上,PO= ![]() 百米.
百米. 
(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道PQ最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设区间D=[﹣3,3],定义在D上的函数f(x)=ax3+bx+1(a>0,b∈R),集合A={a|x∈D,f(x)≥0}.
(1)若b= ![]() ,求集合A;
,求集合A;
(2)设常数b<0 ①讨论f(x)的单调性;
②若b<﹣1,求证:A=.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)令Cn= 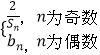 设数列{cn}的前n项和Tn , 求T2n .
设数列{cn}的前n项和Tn , 求T2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 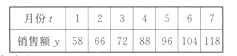
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
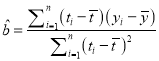 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x||x|<1},N={y|y=2x , x∈M},则集合R(M∩N)等于( )
A.(﹣∞, ![]() ]
]
B.( ![]() ,1)
,1)
C.(﹣∞, ![]() ]∪[1,+∞)
]∪[1,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x,y 满足约束条件 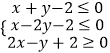 ,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
A.![]() 或﹣1
或﹣1
B.2 或 ![]()
C.2 或1
D.2 或﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com