
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)令Cn= 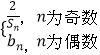 设数列{cn}的前n项和Tn , 求T2n .
设数列{cn}的前n项和Tn , 求T2n .
【答案】解:(Ⅰ)设数列{an}的公差为d,数列{bn}的公比为q, 由b2+S2=10,a5﹣2b2=a3 .
得 ![]() ,解得
,解得 ![]()
∴an=3+2(n﹣1)=2n+1, ![]() .
.
(Ⅱ)由a1=3,an=2n+1得Sn=n(n+2),
则n为奇数,cn= ![]() =
= ![]() ,
,
n为偶数,cn=2n﹣1 .
∴T2n=(c1+c3+…+c2n﹣1)+(c2+c4+…+c2n)
= ![]()
= ![]() =
= ![]()
【解析】(I)利用等差数列与等比数列的通项公式即可得出;(Ⅱ)由a1=3,an=2n+1得Sn=n(n+2).则n为奇数,cn= ![]() =
= ![]() .“分组求和”,利用“裂项求和”、等比数列的前n项和公式即可得出.
.“分组求和”,利用“裂项求和”、等比数列的前n项和公式即可得出.
【考点精析】掌握等差数列的通项公式(及其变式)和等比数列的通项公式(及其变式)是解答本题的根本,需要知道通项公式:![]() 或
或![]() ;通项公式:
;通项公式:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆M:![]() 与
与![]() 轴相切.
轴相切.
(1)求![]() 的值;
的值;
(2)求圆M在![]() 轴上截得的弦长;
轴上截得的弦长;
(3)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作直线
作直线![]() 与圆M相切,
与圆M相切,![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)先将圆的一般方程化成标准方程,利用直线和圆相切进行求解;(2) 令![]() ,得到关于
,得到关于![]() 的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
试题解析:(1) ![]() ∵圆M:
∵圆M:![]() 与
与![]() 轴相切
轴相切
∴![]() ∴
∴![]()
(2) 令![]() ,则
,则![]() ∴
∴![]()
∴![]()
(3) ![]()
∵![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() ∴
∴![]()
∴四边形![]() 面积的最小值为
面积的最小值为![]() .
.
【题型】解答题
【结束】
20
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.
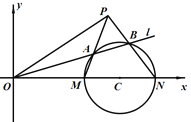
(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(ⅰ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
,
是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用 (基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费
元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费![]() 基准保费
基准保费![]() (
(![]() 浮动比率
浮动比率![]() ).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:
).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:

某机构为了研究某一品牌普通6座以下私家车的投保情况,为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数,得到下面的柱状图:

已知小明家里有一辆该品牌普通6座以下私家车且需要续保,续保费用为![]() 元.
元.
(1)记![]() 为事件“
为事件“![]() ”,求
”,求![]() 的估计值;
的估计值;
(2)求![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]()
![]() 经过点
经过点 ![]() ,其离心率
,其离心率 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设动直线 ![]() 与椭圆
与椭圆 ![]() 相切,切点为
相切,切点为 ![]() ,且
,且 ![]() 与直线
与直线 ![]() 相交于点
相交于点 ![]() .
.
试问:在 ![]() 轴上是否存在一定点,使得以
轴上是否存在一定点,使得以 ![]() 为直径的圆恒过该定点?若存在,
为直径的圆恒过该定点?若存在,
求出该点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 、
、 ![]() ,短轴两个端点为
,短轴两个端点为 ![]() 、
、 ![]() ,且四边形
,且四边形 ![]() 是边长为2的正方形.
是边长为2的正方形.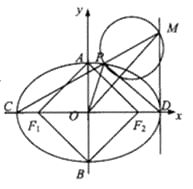
(1)求椭圆的方程;
(2)若 ![]() 、
、 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问 ![]() 轴上是否存异于点
轴上是否存异于点 ![]() 的定点
的定点 ![]() ,使得以
,使得以 ![]() 为直径的圆恒过直线
为直径的圆恒过直线 ![]() 、
、 ![]() 的交点,若存在,求出点
的交点,若存在,求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)= ![]() +bx(a≠0)
+bx(a≠0)
(Ⅰ)若a=﹣2时,函数h(x)=f(x)﹣g(x)在其定义域内是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设φ(x)=e2x+bex , x∈[0,ln2],求函数φ(x)的最小值;
(Ⅲ)设函数f(x)的图象C1与函数g(x)的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com