
【题目】如下图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,平面
的正方形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,且
中点,且![]() .
.
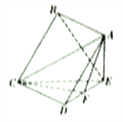
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】试题分析:(I)由中位线定理得出![]() ,故
,故![]() 平面ACF;
平面ACF;
(Ⅱ)由面面垂直的性质得出![]() 平面CDE,故而
平面CDE,故而![]() ,又
,又![]() ,于是
,于是![]() 平面DAE,从而
平面DAE,从而![]() ;
;
(Ⅲ)过F作![]() 于点M,连接CM,,则可证
于点M,连接CM,,则可证![]() 平面ABCD,于是
平面ABCD,于是![]() 为所求的线面角,利用勾股定理和相似三角形求出
为所求的线面角,利用勾股定理和相似三角形求出![]() ,
, ![]() ,得出
,得出![]() .
.
试题解析:(Ⅰ)证明:如下图,连接BD和AC交于点O,
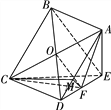
连接OF,
![]() 为正方形,
为正方形,
![]() 为BD的中点,
为BD的中点,
![]() 为DE的中点,
为DE的中点,
![]() ,
,
![]() 平面ACF,
平面ACF,
![]() 平面ACF,
平面ACF,
![]() 平面ACF.
平面ACF.
(Ⅱ)证明: ![]() 平面CDE,
平面CDE,
![]() 平面CDE,
平面CDE,
![]() ,
,
![]() 为正方形,
为正方形,
![]() ,
,
![]() ,AD,
,AD, ![]() 平面DAE,
平面DAE,
![]() 平面DAE,
平面DAE,
![]() 平面DAE,
平面DAE,
![]() .
.
(Ⅲ)解:如图,过F作![]() 于点M,连接CM,
于点M,连接CM,
![]() 平面DAE,
平面DAE, ![]() 平面ABCD,
平面ABCD,
![]() 平面DAE,
平面DAE,
又![]() 平面
平面![]() ,
, ![]() ,
,
![]() 平面ABCD,
平面ABCD,
![]() 是FC在平面ABCD上的射影,
是FC在平面ABCD上的射影,
![]() 是FC与平面ABCD所成角,
是FC与平面ABCD所成角,
![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 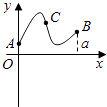
A.
B.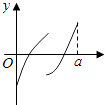
C.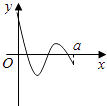
D.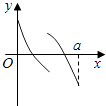
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+(1﹣a) x2﹣a(a+2)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是﹣3,求a,b的值;
(2)若函数f(x)在区间(﹣1,1)上不单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景区的景点A处和B处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从A处出发,以50m/min的速度匀速步行,30min后到达B处,在B处停留20min后,再乘坐缆车回到A处.假设缆车匀速直线运动的速度为150m/mm.
(1)求该游客离景点A的距离y(m)关于出发后的时间x(mm)的函数解析式,并指出该函数的定义域;
(2)做出(1)中函数的图象,并求该游客离景点A的距离不小于1000m的总时长. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 a∈R,函数 f(x)=a﹣ ![]() .
.
(1)证明:f(x)在(﹣∞,+∞)上单调递增;
(2)若f(x)为奇函数,求:
①a的值;
②f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市2016年11月1日![]() 11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
| 2 |
|
| 1 |
|
| 4 |
|
| 6 |
|
| 10 |
|
| ||
| 2 |
|
(Ⅰ)完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污染指数在0![]() 50之间时,空气质量为优;在51
50之间时,空气质量为优;在51![]() 100之间时为良;在101
100之间时为良;在101![]() 150之间时,为轻微污染;在151
150之间时,为轻微污染;在151![]() 200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,即
,即![]() .
.
(1)若数列![]() 为首项为2016,公比为
为首项为2016,公比为![]() 的等比数列,
的等比数列,
①求![]() 的表达式;②当
的表达式;②当![]() 为何值时,
为何值时, ![]() 取得最大值;
取得最大值;
(2)当![]() 时,数列
时,数列![]() 都有
都有![]() 且
且![]() 成立,
成立,
求证: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或下满6局时停止.设甲在每局中获胜的概率为p(p> ![]() ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 ![]() .
.
(1)求p的值;
(2)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com