D
分析:把圆C的方程化为标准方程,找出圆心坐标和半径r,分两种情况考虑:当直线l的斜率不存在时,可得直线l即为y轴,满足被圆C截得的弦长为2,此时直线l为90°;当直线l的斜率存在时,设直线k的斜率为k,又直线l过原点,表示出直线l的方程,利用点到直线的距离公式表示出圆心到直线l的距离d,由垂径定理及勾股定理得出d与r的关系式,将表示出的d及已知的r代入,得到关于k的方程,求出方程的解可得出k的值,再根据直线倾斜角与斜率的关系可得此时直线l的倾斜角,综上,得到所有满足题意的直线l的倾斜角的大小.
解答:将圆C化为标准方程得:(x-1)
2+(y+

)
2=2,
∴圆心坐标为(1,-

),半径r=

,
当直线l的斜率不存在时,显然直线l为y轴时,满足题意,此时l的倾斜角为90°;
当直线l的斜率存在时,设斜率为k,又直线l过原点,
∴直线l的方程为y=kx,即kx-y=0,
∴圆心到直线的距离d=

,又r=

,
∴2=2

,即r
2=d
2+1,
∴
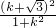
+1=(

)
2,
整理得:1+k
2=k
2+2

k+3,即2

k=-2,
解得:k=-

,
设此时直线l的倾斜角为α,则有tanα=k=-

,
∴α=150°,
综上,l的倾斜角大小为90°或150°.
故选D
点评:此题考查了直线与圆的位置关系,以及直线倾斜角与斜率的关系,涉及的知识有:点到直线的距离公式,圆的标准方程,垂径定理,勾股定理,以及特殊角的三角函数值,利用了分类讨论的思想,当直线与圆相交时,常常利用垂径定理由垂直得出中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

 y+2=0截得的弦长为2,则l的倾斜角大小为
y+2=0截得的弦长为2,则l的倾斜角大小为 )2=2,
)2=2, ),半径r=
),半径r= ,
, ,又r=
,又r= ,
, ,即r2=d2+1,
,即r2=d2+1,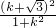 +1=(
+1=( )2,
)2, k+3,即2
k+3,即2 k=-2,
k=-2, ,
, ,
,
