
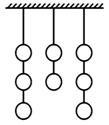
在一次射击比赛中,8个泥制的靶子挂成三列(如图),其中有两列各挂3个,一列挂2个,一位射手按照下列规则去击碎靶子:先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,若每次射击都严格执行这一规则,击碎全部8个靶子的不同方法有

A.560 B.320 C.650 D.360
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 10、在一次射击比赛中,8个泥制的靶子挂成三列(如图),其中有两列各挂3个,一列挂2个,一位射手按照下列规则去击碎靶子:先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,若每次射击都严格执行这一规则,击碎全部8个靶子的不同方法有( )
10、在一次射击比赛中,8个泥制的靶子挂成三列(如图),其中有两列各挂3个,一列挂2个,一位射手按照下列规则去击碎靶子:先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,若每次射击都严格执行这一规则,击碎全部8个靶子的不同方法有( )查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
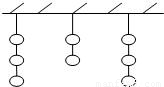
科目:高中数学 来源:2012-2013学年安徽省安庆市太湖二中高三(上)月考数学试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
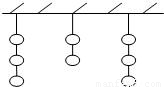
科目:高中数学 来源:2009-2010学年安徽省安庆市桐城中学高三(上)第二次月考数学试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com