
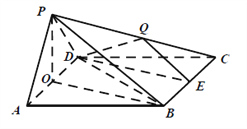
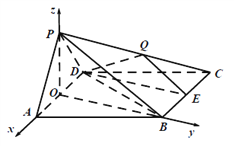
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() 60°,
60°, ![]() ,
, ![]() 是
是![]() 中点,点
中点,点![]() 在侧棱
在侧棱![]() 上.
上.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)是否存在![]() ,使平面
,使平面![]()
![]() 平面
平面![]() ?若存在,求出,若不存在,说明理由.
?若存在,求出,若不存在,说明理由.
(Ⅲ)是否存在![]() ,使
,使![]() 平面
平面![]() ?若存在,求出.若不存在,说明理由.
?若存在,求出.若不存在,说明理由.

【答案】(I)详见解析;(II)详见解析;(III)详见解析.
【解析】试题分析:(1)取![]() 中点
中点![]() ,通过证明
,通过证明![]() 平面
平面![]() ,可证
,可证![]() 。(2)以
。(2)以![]() 为坐标原点,OA,OB,OP分别为x,y,z轴建立空间直角坐标系,用空间向量法寻找点Q.(3)由(2)用空间向量法寻找点Q.
为坐标原点,OA,OB,OP分别为x,y,z轴建立空间直角坐标系,用空间向量法寻找点Q.(3)由(2)用空间向量法寻找点Q.
试题解析:
(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() .
.
因为![]() ,所以
,所以![]() .
.
因为菱形![]() 中,
中, ![]() ,所以
,所以![]() .
.
所以![]() .
.
因为![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)由(Ⅰ)可知, ![]() ,
,
因为侧面![]() 底面
底面![]() ,且平面
,且平面![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() .
.
以![]() 为坐标原点,如图建立空间直角坐标系
为坐标原点,如图建立空间直角坐标系![]() .
.
则![]() ,因为
,因为![]() 为
为![]() 中点,所以
中点,所以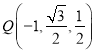 .
.
所以 ,所以平面
,所以平面![]() 的法向量为
的法向量为![]() .
.
因为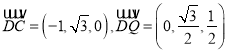 ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则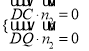 ,即
,即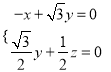 .
.
令![]() ,则
,则![]() ,即
,即![]() .
.
所以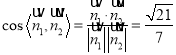 .
.
由图可知,二面角![]() 为锐角,所以余弦值为
为锐角,所以余弦值为![]() .
.
(Ⅲ)设![]()
由(Ⅱ)可知![]() .
.
设![]() ,则
,则![]() ,
,
又因为![]() ,所以
,所以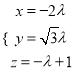 ,即
,即![]() .
.
所以在平面![]() 中,
中, ![]() ,
,
所以平面![]() 的法向量为
的法向量为![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
即![]() ,解得
,解得![]() .
.
所以当![]() 时,
时, ![]() 平面
平面![]()


科目:高中数学 来源: 题型:
【题目】根据教育部最新消息,2020年高考数学将是最后一年实行文理分科,由于课程大纲与命题方向出现了变动,试题难度也可能会做出相应调整.为了评估学生在2020年高考复习情况,某中学组织本校540名考生参加市模拟考试,现采用分层抽样的方法从文、理科考生中分别抽取60和30份数学试卷进行成绩分析,得到下面的成绩频数分布表:
分数分组 |
|
|
|
|
|
文科频数 | 12 | 4 | 10 | 11 | 23 |
理科频数 | 3 | 7 | 2 | 10 | 8 |
由此可估计文科考生的不及格人数(90分为及格分数线)大约为( )
A.128B.156C.204D.132
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角![]() 的三边长
的三边长![]() ,满足
,满足![]() .
.
(Ⅰ)在![]() 之间插入
之间插入![]() 个数,使这
个数,使这![]() 个数构成以
个数构成以![]() 为首项的等差数列
为首项的等差数列![]() ,且它们的和为
,且它们的和为![]() ,求斜边的最小值;
,求斜边的最小值;
(Ⅱ)已知![]() 均为正整数,且
均为正整数,且![]() 成等差数列,将满足条件的三角形的面积从小到大排成一列
成等差数列,将满足条件的三角形的面积从小到大排成一列![]() ,且
,且![]() ,求满足不等式
,求满足不等式![]() 的所有
的所有![]() 的值;
的值;
(Ⅲ)已知![]() 成等比数列,若数列
成等比数列,若数列![]() 满足
满足![]() ,证明:数列
,证明:数列![]() 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且![]() 是正整数.
是正整数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,

(1)求证:CF∥平面A1DE;
(2)求平面A1DE与平面A1DA夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某银行对某市最近5年住房贷款发放情况(按每年6月份与前一年6月份为1年统计)作了统计调查,得到如下数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
贷款 | 50 | 60 | 70 | 80 | 100 |
(1)将上表进行如下处理:![]() ,
,
得到数据:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
试求![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,再写出
,再写出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() .
.
(2)利用(1)中所求的线性回归方程估算2019年房贷发放数额.
参考公式: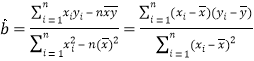 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上一个圆可以将平面分成两个部分,两个圆最多可以将平面分成4个部分,设平面上![]() 个圆最多可以将平面分成
个圆最多可以将平面分成![]() 个部分.
个部分.
![]() 求
求![]() ,
,![]() 的值;
的值;
![]() 猜想
猜想![]() 的表达式并证明;
的表达式并证明;
![]() 证明:
证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com