Question

【题目】已知直角的三边长,满足.

（Ⅰ）在之间插入个数,使这个数构成以为首项的等差数列,且它们的和为,求斜边的最小值;

（Ⅱ）已知均为正整数,且成等差数列,将满足条件的三角形的面积从小到大排成一列,且,求满足不等式的所有的值;

（Ⅲ）已知成等比数列,若数列满足,证明:数列中的任意连续三项为边长均可以构成直角三角形,且是正整数.

Answer 1

【答案】（1）（2）（3）见解析

解:（Ⅰ）是等差数列, ,即.

,斜边的最小值为 (当且仅当等号成立,

此时数列中, .

（Ⅱ）设的公差为,则,.

设三角形的三边长为面积,

,

由得.

当时, ,

经检验当时, ,当时, ,

综上所述,满足不等式的所有的值为.

（Ⅲ）证明:因为成等比数列, ,

因为为直角三角形的三边长,知,

又,得,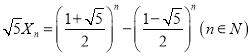

于是,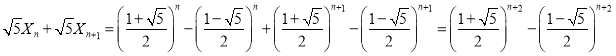

,

则有,

故数列中的任意连续三项为边长均可以构成直角三角形.

因为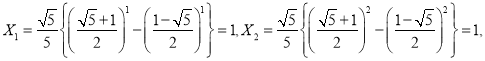

,

由,同理可得,

故对于任意的都有是正整数.

【解析】试题分析：（Ⅰ） 是等差数列, ,即.．

利用勾股定理与基本不等式的性质即可得出．
（Ⅱ）设的公差为,则,.

设三角形的三边长为面积,

,利用等差数列的求和公式可得．由得，经过分类讨论即可得出．

（Ⅲ）由成等比数列, ,因为为直角三角形的三边长,

知,

又,，可得，再利用勾股定理进行验证即可得出．

试题解析：

（Ⅰ）是等差数列, ,即.

,斜边的最小值为 (当且仅当等号成立,

此时数列中, .

（Ⅱ）设的公差为,则,.

设三角形的三边长为面积,

,

由得.

当时, ,

经检验当时, ,当时, ,

综上所述,满足不等式的所有的值为.

（Ⅲ）证明:因为成等比数列, ,

因为为直角三角形的三边长,知,

又,得,

于是,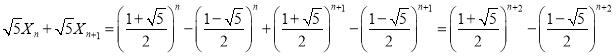

,

则有,

故数列中的任意连续三项为边长均可以构成直角三角形.

因为

,

由,同理可得,

故对于任意的都有是正整数.