
【题目】已知函数y=f(x)是R上的偶函数,且当x≤0时,f(x)=log ![]() (1﹣x)+x.
(1﹣x)+x.
(1)求f(1)的值;
(2)求函数y=f(x)的表达式,并直接写出其单调区间(不需要证明);
(3)若f(lga)+2<0,求实数a的取值范围.
【答案】
(1)解:f(1)=f(﹣1)=﹣2
(2)解:令x>0,则﹣x<0,
则f(﹣x)= log ![]() (1+x)﹣x=f(x),
(1+x)﹣x=f(x),
故x>0时,f(x)= log ![]() (1+x)﹣x,
(1+x)﹣x,
故f(x)=  ;
;
故f(x)在(﹣∞,0]递增,在(0,+∞)递减
(3)解:若f(lga)+2<0,即f(lga)<﹣2,
lga>0时,f(lga)<f(1),则lga>1,
lga<0时,f(lga)<f(﹣1),则lga<﹣1,
故lga>1或lga<﹣1,
解得:a>10或0<a< ![]()
【解析】(1)根据函数的奇偶性求出f(1)即f(﹣1)的值即可;(2)令x>0,得到﹣x<0,根据函数的奇偶性求出f(x)的解析式,从而求出函数的单调区间即可;(3)问题转化为f(lga)<﹣2,得到关于a的不等式,解出即可.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为预防H1N1病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如表:
A组 | B组 | C组 | |
疫苗有效 | 673 | x | y |
疫苗无效 | 77 | 90 | z |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y≥465,z≥25,求不能通过测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)(ω>0,||< ![]() ,x∈R)的部分图象如图所示,则函数表达式为( )
,x∈R)的部分图象如图所示,则函数表达式为( ) 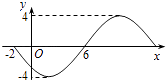
A.y=﹣4sin( ![]() )
)
B.y=4sin( ![]() )
)
C.y=﹣4sin( ![]() )
)
D.y=4sin( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果,其中某班级的正确率为 ![]() ,背诵错误的概率为
,背诵错误的概率为 ![]() ,现记“该班级完成n首背诵后总得分为Sn”.
,现记“该班级完成n首背诵后总得分为Sn”.
(1)求S6=20且Si≥0(i=1,2,3)的概率;
(2)记ξ=|S5|,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
: 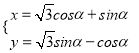 (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)曲线![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】排列组合
(1)7位同学站成一排,甲、乙两同学必须相邻的排法共有多少种?
(2)7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?
(3)7位同学站成一排,甲不站排头,乙不站排尾,不同站法种数有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com