
【题目】已知集合M是满足下列性质的函数![]() 的全体;在定义域内存在实数t,使得
的全体;在定义域内存在实数t,使得![]() .
.
(1)判断![]() 是否属于集合M,并说明理由;
是否属于集合M,并说明理由;
(2)若![]() 属于集合M,求实数a的取值范围;
属于集合M,求实数a的取值范围;
(3)若![]() ,求证:对任意实数b,都有
,求证:对任意实数b,都有![]() .
.
【答案】(1)不属于,理由详见解析;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)利用f(x)=3x+2,通过f(t+2)=f(t)+f(2)推出方程无解,说明f(x)=3x+2不属于集合M;
(2)由![]() 属于集合M,推出
属于集合M,推出![]() 有实解,即(a﹣6)x2+4ax+6(a﹣2)=0有实解,对参数分类讨论,利用判断式求解即可;
有实解,即(a﹣6)x2+4ax+6(a﹣2)=0有实解,对参数分类讨论,利用判断式求解即可;
(3)当f(x)=2x+bx2时,方程f(x+2)=f(x)+f(2)3×2x+4bx﹣4=0,令g(x)=3×2x+4bx﹣4,则g(x)在R上的图象是连续的,当b≥0时,当b<0时,判断函数是否有零点,证明对任意实数b,都有f(x)∈M.
解:(1)当![]() 时,方程
时,方程![]()
此方程无解,所以不存在实数t,使得![]() ,
,
故![]() 不属于集合M﹒
不属于集合M﹒
(2)由![]() ,属于集合M,可得
,属于集合M,可得
方程![]() 有实解
有实解
![]() 有实解
有实解![]() 有实解,
有实解,
若![]() 时,上述方程有实解;
时,上述方程有实解;
若![]() 时,有
时,有![]() ,解得
,解得![]() ,
,
故所求a的取值范围是![]() .
.
(3)当![]() 时,方程
时,方程![]()
![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上的图像是连续的,
上的图像是连续的,
当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 在
在![]() 内至少有一个零点
内至少有一个零点
当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 在
在![]() 内至少有一个零点
内至少有一个零点
故对任意的实数b,![]() 在
在![]() 上都有零点,即方程
上都有零点,即方程![]() 总有解,
总有解,
所以对任意实数b,都有![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾种类可分为可回收垃圾、干垃圾、湿垃圾、有害垃圾等,为调查中学生对垃圾分类的了解程度,某调查小组随机从本市一中高一的![]() 名学生(其中女生
名学生(其中女生![]() 人)中,采用分层抽样的方法抽取
人)中,采用分层抽样的方法抽取![]() 名学生进行调查,已知抽取的
名学生进行调查,已知抽取的![]() 名学生中有男生
名学生中有男生![]() 人、
人、
(1)求![]() 值及抽到的女生人数;
值及抽到的女生人数;
(2)调查小组请这![]() 名学生指出生活中若干项常见垃圾的种类,把能准确分类不少于
名学生指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”,调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”,调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男生(人) | 4 | 22 | 34 | 18 | 16 | 10 | 6 |
女生(人) | 0 | 15 | 20+m | 20 | 16 | 9 | m |
求![]() 值,完成如下
值,完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为学生对垃圾分类的了解程度与性别有关?
的把握认为学生对垃圾分类的了解程度与性别有关?
不太了解 | 比较了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
(3)在(2)条件下,从抽取的“比较了解”的学生中仍采用分层抽样的方法抽取![]() 名.再从这
名.再从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人作义务讲解员,求抽取的
人作义务讲解员,求抽取的![]() 人中至少一名女生的概率.
人中至少一名女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
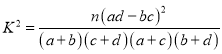 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由![]() 个不同的数构成的数列
个不同的数构成的数列![]() 中,若
中,若![]() 时,
时,![]() (即后面的项
(即后面的项![]() 小于前面项
小于前面项![]() ),则称
),则称![]() 与
与![]() 构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为
构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为![]() ;同理,等比数列
;同理,等比数列![]() 的逆序数为
的逆序数为![]() .
.
(1)计算数列![]() 的逆序数;
的逆序数;
(2)计算数列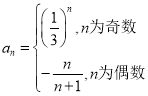 (
(![]() )的逆序数;
)的逆序数;
(3) 已知数列![]() 的逆序数为
的逆序数为![]() ,求
,求![]() 的逆序数.
的逆序数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 行数表如下:
行数表如下:
第一行:![]()
第二行:![]()
第三行:![]()
…… …… ……
第![]() 行:
行:![]()
第m行:![]()
按照上述方式从第一行写到第m行(写下的第n个数记作![]() )得到有穷数列
)得到有穷数列![]() ,其前n项和为
,其前n项和为![]() ,若
,若![]() 存在,则
存在,则![]() 的最小值为______
的最小值为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为
的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为![]() ,且
,且![]() .
.
(1)求椭圆C的方程;
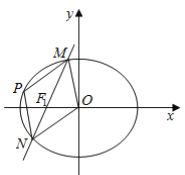
(2)过椭圆C的左焦点![]() 的直线
的直线![]() 交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线
交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”)是现在商家一种常见促销手段.今年“双十一”期间,甲、乙、丙、丁四位顾客在商场购物时,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位顾客对游戏中奖结果进行了预测,预测结果如下:
甲说:“我或乙能中奖”;
乙说:“丁能中奖”;
丙说:“我或乙能中奖”;
丁说:“甲不能中奖”.
游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com