
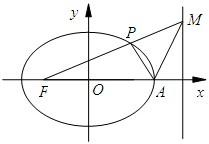
已知椭圆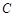 :
: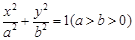 的离心率为
的离心率为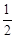 ,右焦点为
,右焦点为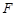 ,右顶点
,右顶点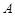 在圆
在圆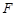 :
: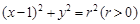 上.
上.
(Ⅰ)求椭圆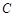 和圆
和圆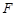 的方程;
的方程;
(Ⅱ)已知过点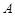 的直线
的直线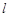 与椭圆
与椭圆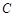 交于另一点
交于另一点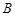 ,与圆
,与圆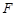 交于另一点
交于另一点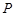 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线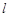 ,使点
,使点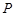 恰好为线段
恰好为线段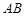 的中点,若存在,求出直线
的中点,若存在,求出直线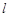 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(Ⅰ) ,
,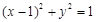 ;(Ⅱ)不存在
;(Ⅱ)不存在
【解析】
试题分析:(Ⅰ)由圆 方程可知圆心为
方程可知圆心为 ,即
,即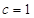 ,又因为离心率为
,又因为离心率为 ,可得
,可得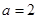 ,根据椭圆中关系式
,根据椭圆中关系式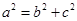 ,可求
,可求 。椭圆方程即可求出。因为
。椭圆方程即可求出。因为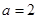 ,则右顶点为
,则右顶点为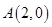 ,将其代入圆的方程可求半径
,将其代入圆的方程可求半径 。(Ⅱ)设出直线方程
。(Ⅱ)设出直线方程 ,然后和椭圆方程联立,消掉y(或x)得到关于x的一元二次方程。再根据韦达定理得出根与系数的关系。因为
,然后和椭圆方程联立,消掉y(或x)得到关于x的一元二次方程。再根据韦达定理得出根与系数的关系。因为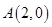 是其中一个交点,所以方程的一个根为2。用中点坐标公式求点
是其中一个交点,所以方程的一个根为2。用中点坐标公式求点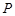 的坐标,再将其代入圆
的坐标,再将其代入圆 方程。解出
方程。解出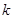 的值。若
的值。若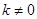 则说明存在满足条件的直线
则说明存在满足条件的直线 可求出其方程,若
可求出其方程,若 ,则说明不存在满足条件的直线
,则说明不存在满足条件的直线 。法二:假设存在,由已知可得
。法二:假设存在,由已知可得 ,因为点
,因为点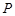 为线段
为线段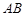 的中点,所以
的中点,所以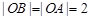 ,因为点
,因为点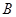 在椭圆上可推导得
在椭圆上可推导得 ,与
,与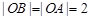 矛盾,故假设不成立。
矛盾,故假设不成立。
试题解析:(Ⅰ)由题意可得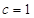 ,
1分
,
1分
又由题意可得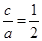 ,
,
所以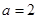 ,
2分
,
2分
所以 ,
3分
,
3分
所以椭圆 的方程为
的方程为 .
4分
.
4分
所以椭圆 的右顶点
的右顶点 ,
5分
,
5分
代入圆 的方程,可得
的方程,可得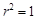 ,
,
所以圆 的方程为
的方程为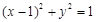 .
6分
.
6分
(Ⅱ)法1:
假设存在直线 :
:
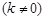 满足条件,
7分
满足条件,
7分
由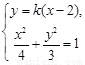 得
得 8分
8分
设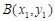 ,则
,则 ,
9分
,
9分
可得中点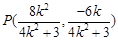 ,
11分
,
11分
由点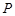 在圆
在圆 上可得
上可得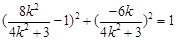
化简整理得 13分
13分
又因为 ,
,
所以不存在满足条件的直线 .
14分
.
14分
(Ⅱ)法2:
假设存在直线 满足题意.
满足题意.
由(Ⅰ)可得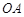 是圆
是圆 的直径,
7分
的直径,
7分
所以 .
8分
.
8分
由点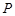 是
是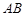 中点,可得
中点,可得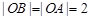 .
9分
.
9分
设点 ,则由题意可得
,则由题意可得 .
10分
.
10分
又因为直线 的斜率不为0,所以
的斜率不为0,所以 ,
11分
,
11分
所以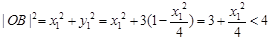 ,
13分
,
13分
这与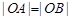 矛盾,所以不存在满足条件的直线
矛盾,所以不存在满足条件的直线 .
14分
.
14分
考点:椭圆及圆的基础知识、直线与椭圆的位置关系,考查分析问题、解决问题以及化归与转化的能力,考查综合素质。


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
 已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若
已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若| |PF1| |
| |PF2| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
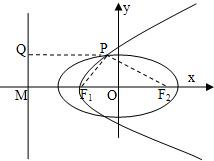
 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |PF1| |
| |PF2| |
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 3 |
3
| ||
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |PF1| |
| |PF2| |
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com