
【题目】窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一.图中的窗花是由一张圆形纸片剪去一个正十字形剩下的部分,正十字形的顶点都在圆周上.已知正十字形的宽和长都分别为x,y(单位:dm)且x<y,若剪去的正十字形部分面积为4dm2.
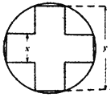
(1)求y关于x的函数解析式,并求其定义域;
(2)现为了节约纸张,需要所用圆形纸片面积最小.当x取何值时,所用到的圆形纸片面积最小,并求出其最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
![]()
根据以上数据,绘制了散点图.
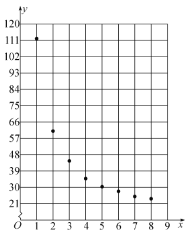
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .参考数据(其中
.参考数据(其中![]() ):
):

(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: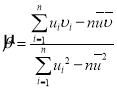 ,
,![]() ,相关系数
,相关系数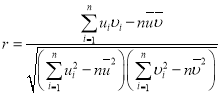 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程是:
的极坐标方程是:![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程.
的直角坐标方程.
(2)点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值与最小值.
距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组,![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
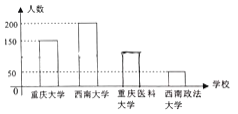
(1)分别求出从重庆大学、西南大学、重庆医科大学、西南政法大学抽出的志愿者人数;
(2)若“嘉宾”小组的2名志愿者只能从重庆医科大学或西南政法大学抽出,求这2人分别来自不同大学的概率(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018 年1月16日,由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓,某知名网站财经频道为了解公众对这些年度人物是否了解,利用网络平台进行了调查,并从参与调查者中随机选出![]() 人,把这
人,把这![]() 人分为
人分为![]() 两类(
两类(![]() 类表示对这些年度人物比较了解,
类表示对这些年度人物比较了解,![]() 类表示对这些年度人物不太了解),并制成如下表格:
类表示对这些年度人物不太了解),并制成如下表格:
年龄段 |
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
(1)若按照年龄段进行分层抽样,从这![]() 人中选出
人中选出![]() 人进行访谈,并从这
人进行访谈,并从这![]() 人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在
人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间,另一名幸运者的年龄在
岁之间,另一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间的概率;(注:从
岁之间的概率;(注:从![]() 人中随机选出
人中随机选出![]() 人,共有
人,共有![]() 种不同选法)
种不同选法)
(2)如果把年龄在![]() 岁~
岁~![]() 岁之间的人称为青少年,年龄在
岁之间的人称为青少年,年龄在![]() 岁~
岁~![]() 岁之间的人称为中老年,则能否在犯错误的概率不超过
岁之间的人称为中老年,则能否在犯错误的概率不超过![]() 的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项都是正数,若对于任意的正整数
的各项都是正数,若对于任意的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,则称函数
成等比数列,则称函数![]() 为“
为“![]() 型”数列.
型”数列.
(1)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”数列,又是“
型”数列,又是“![]() 型”数列,求证:数列
型”数列,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com