
【题目】已知函数f(x)满足![]() ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:设x∈(﹣1,0),则(x+1)∈(0,1),由于当x∈[0,1]时,f(x)=x,可得f(x+1)
=x+1.利用f(x)+1=![]() ,可得f(x)=
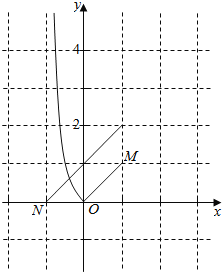
,可得f(x)=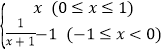 ,方程f(x)﹣mx﹣x=0,化为f(x)=mx+m,画出图象y=f(x),y=m(x+1),M(1,1),N(﹣1,0),可得kMN=
,方程f(x)﹣mx﹣x=0,化为f(x)=mx+m,画出图象y=f(x),y=m(x+1),M(1,1),N(﹣1,0),可得kMN=![]() .即可得出.
.即可得出.
详解:设x∈(﹣1,0),则(x+1)∈(0,1),
∵当x∈[0,1]时,f(x)=x,
∴f(x+1)=x+1.
∵f(x)+1=![]() ,可得f(x)=
,可得f(x)=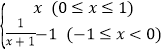 ,
,
方程f(x)﹣mx﹣x=0,化为f(x)=mx+m,
画出图象y=f(x),y=m(x+1),M(1,1),N(﹣1,0),
可得kMN=![]() .
.
∵在区间(﹣1,1]上方程f(x)﹣mx﹣x=0有两个不同的实根,
∴![]() ,
,
故答案为:D


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() N
N![]() ,
,![]() ≥2,且
≥2,且![]() R.
R.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,令
时,令![]() ,若函数
,若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,试求函数
时,试求函数![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,短轴的两个端点分别为A,B,且满足:
,短轴的两个端点分别为A,B,且满足:![]() ,且椭圆经过点
,且椭圆经过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点M![]() 的动直线
的动直线![]() (与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线
(与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线![]() 如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】麻团又叫煎堆,呈球形,华北地区称麻团,是一种古老的中华传统特色油炸面食,寓意团圆。制作时以糯米粉团炸起,加上芝麻而制成,有些包麻茸、豆沙等馅料,有些没有。一个长方体形状的纸盒中恰好放入4个球形的麻团,它们彼此相切,同时与长方体纸盒上下底和侧面均相切,其俯视图如图所示,若长方体纸盒的表面积为576 ![]() ,则一个麻团的体积为_______
,则一个麻团的体积为_______![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查人们在购物时的支付习惯,某超市对随机抽取的600名顾客的支付方式进行了统计,数据如下表所示:
支付方式 | 微信 | 支付宝 | 购物卡 | 现金 |
人数 | 200 | 150 | 150 | 100 |
现有甲、乙、丙三人将进入该超市购物,各人支付方式相互独立,假设以频率近似代替概率.
(1)求三人中使用微信支付的人数多于现金支付人数的概率;
(2)记![]() 为三人中使用支付宝支付的人数,求
为三人中使用支付宝支付的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com