练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知某批零件的长度误差(单位：毫米)服从正态分布N(0,32)，从中随机取一件,其长度误差落在区间(3,6)内的概率为(　　)

    (附：若随机变量ξ服从正态分布N(μ，σ2),则P(μ－σ<ξ<μ＋σ)＝68.27%,P(μ－2σ＜ξ＜μ＋2σ)＝95.45%.)

    A. 4.56%B. 13.59%C. 27.18%D. 31.74%

    【答案】B

    【解析】

    由题意P（﹣3＜ξ＜3）＝68.27%，P（﹣6＜ξ＜6）＝95.45%，可得P（3＜ξ＜6）＝（95.45%﹣68.27%），即可得出结论．

    解：由题意P（﹣3＜ξ＜3）＝68.27%，P（﹣6＜ξ＜6）＝95.45%，

    ∴P（3＜ξ＜6）＝（95.45%﹣68.27%）＝13.59%．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】数列满足an＝2an－1＋2n＋1(n∈N*，n≥2)， .

    (1)求的值；

    (2)是否存在一个实数t，使得 (n∈N*)，且数列{}为等差数列？若存在，求出实数t；若不存在，请说明理由；

    (3)求数列的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，一智能扫地机器人在处发现位于它正西方向的处和北偏东30°方向上的处分别有需要清扫的垃圾，红外线感应测量发现机器人到的距离比到的距离少0.4米，于是选择沿路线清扫，已知智能扫地机器人的直线行走速度为0.2，忽略机器人吸入垃圾及在处旋转所用时间，10秒钟完成了清扫任务．

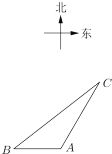
    （1）、两处垃圾的距离是多少？

    （2）智能扫地机器人此次清扫行走路线的夹角的正弦值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，圆的普通方程为. 在以坐标原点为极点，轴正半轴为极轴的极坐标系中，直线的极坐标方程为 .

    （Ⅰ） 写出圆 的参数方程和直线的直角坐标方程；

    （ Ⅱ ） 设直线 与轴和轴的交点分别为，为圆上的任意一点，求的取值范围.

    【答案】(1);.

    (2).

    【解析】【试题分析】(I)利用圆心和半径,写出圆的参数方程,将圆的极坐标方程展开后化简得直角坐标方程.(II)求得两点的坐标, 设点，代入向量,利用三角函数的值域来求得取值范围.

    【试题解析】

    （Ⅰ）圆的参数方程为（为参数）.

    直线的直角坐标方程为.

    （Ⅱ）由直线的方程可得点，点.

    设点，则 .

    .

    由（Ⅰ）知，则 .

    因为，所以.

    【题型】解答题
    【结束】
    23

    【题目】选修4-5：不等式选讲

    已知函数， .

    （Ⅰ）若对于任意， 都满足，求的值；

    （Ⅱ）若存在，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年2月9-25日，第23届冬奥会在韩国平昌举行.4年后，第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会，某大学在平昌冬奥会开幕后的第二天，从全校学生中随机抽取了120名学生，对是否收看平昌冬奥会开幕式情况进行了问卷调查，统计数据如下：

    收看

    没收看

    男生

    60

    20

    女生

    20

    20

    (Ⅰ)根据上表说明，能否有的把握认为，收看开幕式与性别有关？

    (Ⅱ)现从参与问卷调查且收看了开幕式的学生中，采用按性别分层抽样的方法选取8人，参加2022年北京冬奥会志愿者宣传活动.

    (ⅰ)问男、女学生各选取多少人？

    (ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍，求恰好选到一名男生一名女生的概率P.

    附：，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂家具车间造、型两类桌子，每张桌子需木工和漆工梁道工序完成.已知木工做一张、型型桌子分别需要1小时和2小时，漆工油漆一张、型型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张、型型桌子分别获利润2千元和3千元.

    (1)列出满足生产条件的数学关系式，并画出可行域；

    (2)怎样分配生产任务才能使每天的利润最大，最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂家具车间造、型两类桌子，每张桌子需木工和漆工梁道工序完成.已知木工做一张、型型桌子分别需要1小时和2小时，漆工油漆一张、型型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张、型型桌子分别获利润2千元和3千元.

    (1)列出满足生产条件的数学关系式，并画出可行域；

    (2)怎样分配生产任务才能使每天的利润最大，最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:

    打算观看

    不打算观看

    女生

    20

    b

    男生

    c

    25

    （1）求出表中数据b，c;

    （2）判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;

    （3）为了计算“从10人中选出9人参加比赛”的情况有多少种，我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题：在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三（5）班，从中推选5人接受校园电视台采访，请根据上述方法，求被推选出的5人中恰有四名男生、一名女生的概率.

    P(K2≥k0)

    0.10

    0.05

    0.025

    0.01

    0.005

    K0

    2.706

    3.841

    5.024

    6.635

    7.879

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是偶函数，且满足，当时， ，当时， 的最大值为.

    （1）求实数的值；

    （2）函数，若对任意的，总存在，使不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案