
【题目】数列![]() 满足an=2an-1+2n+1(n∈N*,n≥2),
满足an=2an-1+2n+1(n∈N*,n≥2), ![]() .
.
(1)求![]() 的值;
的值;
(2)是否存在一个实数t,使得![]() (n∈N*),且数列{
(n∈N*),且数列{![]() }为等差数列?若存在,求出实数t;若不存在,请说明理由;
}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列![]() 的前n项和
的前n项和![]() .
.
【答案】(1)a1=2,a2=9;(2)t=1;(3)Sn=(2n-1)×2n-n+1.
【解析】试题分析:(1)利用an=2an-1+2n+1, ![]() ,代入可求;
,代入可求;
(2)假设存在实数t,使得{bn}为等差数列,从而有2bn=bn-1+bn+1,代入条件即可得解;
(3)利用错位相减即可得解.
试题解析:
(1)由a3=27,得27=2a2+23+1,∴a2=9,
∵9=2a1+22+1,∴a1=2.
(2)假设存在实数t,使得{bn}为等差数列,
则2bn=bn-1+bn+1(n≥2且n∈N*),
∴2×![]() (an+t)=
(an+t)=![]() (an-1+t)+
(an-1+t)+![]() (an+1+t),
(an+1+t),
∴4an=4an-1+an+1+t,
∴4an=4×![]() +2an+2n+1+1+t,∴t=1.
+2an+2n+1+1+t,∴t=1.
即存在实数t=1,使得{bn}为等差数列.
(3)由(1),(2)得b1=![]() ,b2=
,b2=![]() ,∴bn=n+
,∴bn=n+![]() ,
,
∴an=![]() ·2n-1=(2n+1)2n-1-1,
·2n-1=(2n+1)2n-1-1,
Sn=(3×20-1)+(5×21-1)+(7×22-1)+…+[(2n+1)×2n-1-1]
=3+5×2+7×22+…+(2n+1)×2n-1-n,①
∴2Sn=3×2+5×22+7×23+…+(2n+1)×2n-2n,②
由①-②得-Sn=3+2×2+2×22+2×23+…+2×2n-1-(2n+1)×2n+n=1+2×![]() -(2n+1)×2n+n
-(2n+1)×2n+n
=(1-2n)×2n+n-1,
∴Sn=(2n-1)×2n-n+1.


科目:高中数学 来源: 题型:
【题目】如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
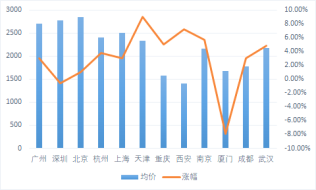
其中结论正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高;
B.深圳和厦门往返机票的平均价格同去年相比有所下降;
C.平均价格从高到低位于前三位的城市为北京,深圳,广州;
D.平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的两个数列![]() 和{
和{![]() }满足:an+1=
}满足:an+1=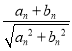 ,n∈N*.
,n∈N*.
(1)设bn+1=1+![]() ,n∈N*,求证:数列
,n∈N*,求证:数列![]() 是等差数列;
是等差数列;
(2)设bn+1=![]() ·
·![]() ,n∈N*,且
,n∈N*,且![]() 是等比数列,求a1和b1的值.
是等比数列,求a1和b1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,底面ABC为等腰直角三角形,
中,底面ABC为等腰直角三角形,![]() ,
,![]() ,
,![]() ,M是侧棱
,M是侧棱![]() 上一点,设
上一点,设![]() ,用空间向量知识解答下列问题.
,用空间向量知识解答下列问题.
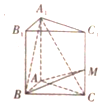
![]() 1
1![]() 若
若![]() ,证明:
,证明:![]() ;
;
![]() 2
2![]() 若
若![]() ,求直线
,求直线![]() 与平面ABM所成的角的正弦值.
与平面ABM所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为( )
(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.27%,P(μ-2σ<ξ<μ+2σ)=95.45%.)
A. 4.56%B. 13.59%C. 27.18%D. 31.74%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com