
【题目】在极坐标系中,点![]() 的极坐标是
的极坐标是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,斜率为
轴的正半轴建立平面直角坐标系,斜率为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)若![]() 时,写出直线
时,写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 相交于不同的两点
相交于不同的两点![]() ,求线段
,求线段![]() 的中点
的中点![]() 的在直角坐标系中的轨迹方程.
的在直角坐标系中的轨迹方程.
【答案】(1)![]() ;
;![]() (2)
(2)![]() ,
,![]()
【解析】
(1)利用极坐标和直角坐标的互化公式即可得解;
(2)方法一:设直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 的方程联立,根据参数的几何意义求得
的方程联立,根据参数的几何意义求得![]() ,代入直线方程求得
,代入直线方程求得![]() 化简消参即可得出结果.
化简消参即可得出结果.
方法二: 由于直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() ,与曲线
,与曲线![]() 方程联立,根据韦达定理可得
方程联立,根据韦达定理可得![]() ,代入直线求得
,代入直线求得![]() ,化简可得
,化简可得![]() ,即可得出结果.
,即可得出结果.
解:(1)![]() 点的直角坐标为
点的直角坐标为![]() ,所以直线
,所以直线![]()
![]() ,可得
,可得![]() ,
,
即![]()
(2)如图可知,直线和圆相切时,![]() .
.
方法一:设直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数)
为参数)
由于直线![]() 和曲线
和曲线![]() 相交,所以
相交,所以![]()
联立直线![]() 和曲线
和曲线![]() 的方程可得
的方程可得![]()
![]()
所以![]() ,即
,即![]()
因此![]() ,其中
,其中![]()
即点![]() 的轨迹方程为
的轨迹方程为![]() ,
,![]()
方法二:显然直线![]() 的斜率存在,不妨设为
的斜率存在,不妨设为![]() ,即直线
,即直线![]() ,
,
与![]() 联立可得:
联立可得:![]() ,
,
![]() ,可以解得
,可以解得![]() ,即:
,即:![]()
设![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
可得![]()
所以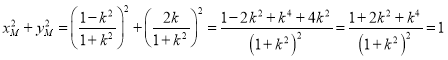
另一方面,由于![]() ,所以
,所以![]()
综上,点![]() 的轨迹方程为
的轨迹方程为![]() ,
,![]()



科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为非零实数,其前
的各项均为非零实数,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对任意正整数
对任意正整数![]() 恒成立,若存在,求实数
恒成立,若存在,求实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校高三年级有1000人参加一次数学模拟考试,现把这次考试的分数转换为标准分,标准分的分数转换区间为![]() ,若使标准分X服从正态分布N
,若使标准分X服从正态分布N![]() ,则下列说法正确的有( ).
,则下列说法正确的有( ).
参考数据:①![]() ;②
;②![]() ;③
;③![]()
A.这次考试标准分超过180分的约有450人
B.这次考试标准分在![]() 内的人数约为997
内的人数约为997
C.甲、乙、丙三人恰有2人的标准分超过180分的概率为![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() ,
,![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() .
.
(1)证明:直线![]() 过定点;
过定点;
(2)若以![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,且切点为线段
相切,且切点为线段![]() 的中点,求该圆的面积.
的中点,求该圆的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,给定下列命题:
,给定下列命题:
①若方程![]() 有两个不同的实数根,则
有两个不同的实数根,则![]() ;
;
②若方程![]() 恰好只有一个实数根,则
恰好只有一个实数根,则![]() ;
;
③若![]() ,总有
,总有![]() 恒成立,则
恒成立,则![]() ;
;
④若函数![]() 有两个极值点,则实数
有两个极值点,则实数![]() .
.
则正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
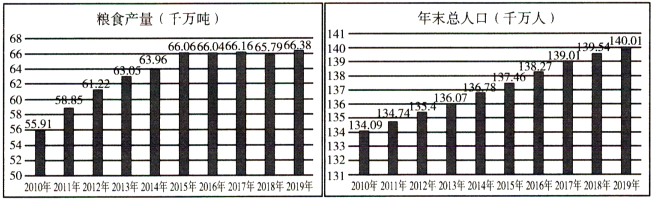
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com