
【题目】在平面直角坐标系中,![]() 为坐标原点.对任意的点
为坐标原点.对任意的点![]() ,定义
,定义![]() .任取点
.任取点![]() ,
,![]() ,记
,记![]() ,
,![]() ,若此时
,若此时![]() 成立,则称点
成立,则称点![]() ,
,![]() 相关.
相关.
(1)分别判断下面各组中两点是否相关,并说明理由;
①![]() ,
,![]() ;②
;②![]() ,
,![]() .
.
(2)给定![]() ,
,![]() ,点集
,点集![]() .
.
(![]() )求集合
)求集合![]() 中与点
中与点![]() 相关的点的个数;
相关的点的个数;
(![]() )若
)若![]() ,且对于任意的
,且对于任意的![]() ,
,![]() ,点
,点![]() ,
,![]() 相关,求
相关,求![]() 中元素个数的最大值.
中元素个数的最大值.
【答案】(1)①相关;②不相关.(2)(![]() )
)![]() 个(
个(![]() )
)![]() .
.
【解析】
(1)根据所给定义,代入不等式化简变形可得对应坐标满足的关系,即可判断所给两个点的坐标是否符合定义要求.
(2)(![]() )根据所给点集,依次判断在四个象限内满足的点个数,坐标轴上及原点的个数,即可求得集合
)根据所给点集,依次判断在四个象限内满足的点个数,坐标轴上及原点的个数,即可求得集合![]() 中与点
中与点![]() 相关的点的个数;(
相关的点的个数;(![]() )由(1)可知相关点满足
)由(1)可知相关点满足![]() ,利用分类讨论证明
,利用分类讨论证明![]() ,即可求得
,即可求得![]() 中元素个数的最大值.
中元素个数的最大值.
若点![]() ,
,![]() 相关,则
相关,则![]() ,
,![]() ,而
,而![]() ,
,
不妨设![]() ,
,
则由定义![]() 可知
可知![]() ,
,
化简变形可得![]() ,
,
(1)对于①![]() ,
,![]() ;对应坐标取绝对值,代入可知
;对应坐标取绝对值,代入可知![]() 成立,因此相关;
成立,因此相关;
②对应坐标取绝对值,代入可知![]() ,因此不相关.
,因此不相关.
(2)(![]() )在第一象限内,
)在第一象限内,![]() ,可知
,可知![]() 且
且![]() ,有
,有![]() 个点;同理可知,在第二象限、第三象限、第四象限也各有
个点;同理可知,在第二象限、第三象限、第四象限也各有![]() 个点.
个点.
在![]() 轴正半轴上,点
轴正半轴上,点![]() 满足条件;在
满足条件;在![]() 轴负半轴上,点
轴负半轴上,点![]() 满足条件;
满足条件;
在![]() 轴正半轴上,点
轴正半轴上,点![]() 满足条件;在
满足条件;在![]() 轴负半轴上,点
轴负半轴上,点![]() 满足条件;
满足条件;
原点![]() 满足条件;
满足条件;
因此集合![]() 中共有
中共有![]() 个点与点
个点与点![]() 相关.
相关.
(![]() )若两个不同的点
)若两个不同的点![]() ,
,![]() 相关,其中
相关,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可知![]() .
.
下面证明![]() .
.
若![]() ,则
,则![]() ,成立;
,成立;
若![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,亦成立.
,亦成立.
由于![]() ,
,
因此最多有![]() 个点两两相关,其中最多有
个点两两相关,其中最多有![]() 个点在第一象限;最少有1个点在坐标轴正半轴上,一个点为原点.
个点在第一象限;最少有1个点在坐标轴正半轴上,一个点为原点.
因此![]() 中元素个数的最大值为
中元素个数的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若曲线![]() 在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
(3)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系.xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C2的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防新型冠状病毒的传染,人员之间需要保持一米以上的安全距离.某公司会议室共有四行四列座椅,并且相邻两个座椅之间的距离超过一米,为了保证更加安全,公司规定在此会议室开会时,每一行、每一列均不能有连续三人就座.例如下图中第一列所示情况不满足条件(其中“√”表示就座人员).根据该公司要求,该会议室最多可容纳的就座人数为( )
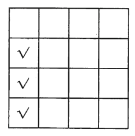
A.9B.10C.11D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农业银行广元分行发行“金穗广元·剑门关旅游卡”是以“游广元、知广元、爱广元、共享和谐广元”为主题活动的一项经济性和公益性相结合的重大举措,以最优惠的价格惠及广元户籍市民、浙江及黑龙江援建省群众、省内援建市市民,凡上述对象均可办理此卡,本人凭此卡及本人身份证一年内(期满后可重新充值办理)在广元市范围内可无限次游览所有售门票景区景点,如:剑门关、朝天明月峡、旺苍鼓城山—七里峡、青川唐家河、广元皇泽寺、苍溪梨博园、昭化古城等,现有浙江及黑龙江援建省群众甲乙两人准备到广元旅游(同游),他们决定游览上面![]() 个景点,首先游览剑门关但不能最后游览朝天明月峡的游览顺序有( )种.
个景点,首先游览剑门关但不能最后游览朝天明月峡的游览顺序有( )种.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 经过点
经过点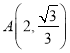 ,两个焦点为
,两个焦点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 是
是![]() 上一点,直线
上一点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,证明:当
,证明:当![]() 点在
点在![]() 上移动时,
上移动时,![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com