
【题目】如图,在![]() 中,
中, ![]() ,角
,角![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,设
,设![]() .(1)求
.(1)求![]() ;(2)若
;(2)若![]() ,求
,求![]() 的长.
的长.
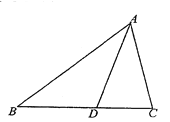
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由α为三角形BAD中的角,根据sinα的值,利用同角三角函数间的基本关系求出cosα的值,进而利用二倍角的正弦函数公式求出sin∠BAC与cos∠BAC的值,即为sin2α与cos2α的值,sinC变形为![]() ,利用诱导公式,以及两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出sinC的值;
,利用诱导公式,以及两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出sinC的值;
(2)利用正弦定理列出关系式,将sinC与sin∠BAC的值代入得出![]() ,利用平面向量的数量积运算法则化简已知等式左边,将表示出的AB代入求出BC的长,再利用正弦定理即可求出AC的长.
,利用平面向量的数量积运算法则化简已知等式左边,将表示出的AB代入求出BC的长,再利用正弦定理即可求出AC的长.
试题解析:
解:(1)∵![]() ,
, ![]() ,
,
∴![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由正弦定理,得![]() ,即
,即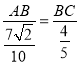 ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,由上两式解得
,由上两式解得![]() ,
,
又由![]() 得
得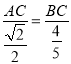 ,∴
,∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
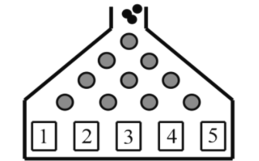
【题目】如图,高尔顿板是英国生物统计学家高尔顿设计的用来研究随机现象的模型,它是在一块竖起的木板上钉上一排排互相平行,水平间隔相等的圆柱形铁钉,并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央,从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两钉的间隙,又碰到下一排铁钉,如此继续下去,在最底层的5个出口处各放置一个容器接住小球,那么,小球落入1号容器的概率是______,若取4个小球进行试验,设其中落入4号容器的小球个数为x,则x的数学期望是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 是面对角线
是面对角线![]() 上两个不同的动点.以下四个命题:①存在
上两个不同的动点.以下四个命题:①存在![]() 两点,使
两点,使![]() ;②存在
;②存在![]() 两点,使
两点,使![]() 与直线
与直线![]() 都成
都成![]() 的角;③若
的角;③若![]() ,则四面体
,则四面体![]() 的体积一定是定值;④若
的体积一定是定值;④若![]() ,则四面体
,则四面体![]() 在该正方体六个面上的正投影的面积的和为定值.其中为真命题的是____.
在该正方体六个面上的正投影的面积的和为定值.其中为真命题的是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的两点,
轴对称的两点,![]() 是
是![]() 的左焦点,
的左焦点,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 过点
过点![]() ,和椭圆
,和椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() .点
.点![]() 坐标是
坐标是![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=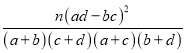 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() ),点
),点![]() 是
是![]() 的左顶点,点
的左顶点,点![]() 为
为![]() 上一点,离心率
上一点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() (异于点
(异于点![]() ),是否存在直线
),是否存在直线![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com