
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 写出
写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的面积.
的面积.
【答案】(Ⅰ)x+y-3=0,x2+y2-4y=0(Ⅱ)![]()
【解析】
(Ⅰ)利用加减消元法,可以消去参数![]() ,得到
,得到![]() 的普通方程,
的普通方程,
利用![]() ,可以把
,可以把![]() 化成直角坐标方程;
化成直角坐标方程;
(Ⅱ)把![]() 化成圆标准方程,求出圆心坐标、半径,利用点到直线距离公式,求出弦心距,利用勾股定理求出弦长,最后求出面积。
化成圆标准方程,求出圆心坐标、半径,利用点到直线距离公式,求出弦心距,利用勾股定理求出弦长,最后求出面积。
解:(Ⅰ)∵曲线C1的参数方程为![]() ,(t为参数),
,(t为参数),
∴C1的普通方程为x+y-3=0,
∵曲线C2的极坐标方程为ρ=4sinθ,即ρ2=4ρsinθ,
∴C2的直角坐标方程为x2+y2-4y=0.
(Ⅱ)原点O到直线x+y-3=0的距离为d=![]() ,
,
C2的标准方程为x2+(y-2)2=4,表示圆心为C2(0,2),半径r=2的圆,
C2到直线x+y-3=0的距离d2=![]() ,
,
∴|AB|=2![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).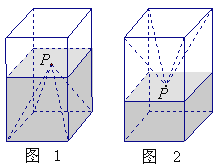
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面定义一个同学数学成绩优秀的标志为:“连续![]() 次考试成绩均不低于
次考试成绩均不低于![]() 分”.现有甲、乙、丙三位同学连续
分”.现有甲、乙、丙三位同学连续![]() 次数学考试成绩的记录数据(记录数据都是正整数):
次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:![]() 个数据的中位数为
个数据的中位数为![]() ,众数为
,众数为![]() ;
;
②乙同学:![]() 个数据的中位数为
个数据的中位数为![]() ,总体均值为
,总体均值为![]() ;
;
③丙同学:![]() 个数据的中位数为
个数据的中位数为![]() ,总体均值为
,总体均值为![]() ,总体方差为
,总体方差为![]() ;
;
则可以判定数学成绩优秀同学为()
A. 甲、丙B. 乙、丙C. 甲、乙D. 甲、乙、丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com