
【题目】如图,已知![]() 、
、![]() 两个城镇相距20公里,设
两个城镇相距20公里,设![]() 是
是![]() 中点,在
中点,在![]() 的中垂线上有一高铁站
的中垂线上有一高铁站![]() ,
,![]() 的距离为10公里.为方便居民出行,在线段
的距离为10公里.为方便居民出行,在线段![]() 上任取一点
上任取一点![]() (点
(点![]() 与
与![]() 、
、![]() 不重合)建设交通枢纽,从高铁站铺设快速路到
不重合)建设交通枢纽,从高铁站铺设快速路到![]() 处,再铺设快速路分别到
处,再铺设快速路分别到![]() 、
、![]() 两处.因地质条件等各种因素,其中快速路
两处.因地质条件等各种因素,其中快速路![]() 造价为1.5百万元/公里,快速路
造价为1.5百万元/公里,快速路![]() 造价为1百万元/公里,快速路
造价为1百万元/公里,快速路![]() 造价为2百万元/公里,设
造价为2百万元/公里,设![]() ,总造价为
,总造价为![]() (单位:百万元).
(单位:百万元).

(1)求![]() 关于
关于![]() 的函数关系式,并指出函数的定义域;
的函数关系式,并指出函数的定义域;
(2)求总造价的最小值,并求出此时![]() 的值.
的值.
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过对本地养鱼场年利润率的调研,其结果是:年利润亏损10%的概率为0.2,年利润获利30%的概率为0.4,年利润获利50%的概率为0.4,对远洋捕捞队的调研结果是:年利润获利为60%的概率为0.7,持平的概率为0.2,年利润亏损20%的可能性为0.1. 为确保本地的鲜鱼供应,市政府要求该公司对远洋捕捞队的投资不得高于本地养鱼场的投资的2倍.根据调研数据,该公司如何分配投资金额,明年两个项目的利润之和最大值为_________千万.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解日益拥堵的交通状况,不少城市实施车牌竞价策略,以控制车辆数量.某地车牌竞价的基本规则是:①“盲拍”,即所有参与竞拍的人都要网络报价一次,每个人不知晓其他人的报价,也不知道参与当期竞拍的总人数;②竞价时间截止后,系统根据当期车牌配额,按照竞拍人的出价从高到低分配名额.某人拟参加2018年5月份的车牌竞拍,他为了预测最低成交价,根据竞拍网站的数据,统计了最近5个月参与竞拍的人数(见下表):

(1)由收集数据的散点图发现,可用线性回归模型拟合竞拍人数y(万人)与月份编号t之间的相关关系.请用最小二乘法求y关于t的线性回归方程:![]() ,并预测2018年5月份参与竞拍的人数.
,并预测2018年5月份参与竞拍的人数.
(2)某市场调研机构从拟参加2018年5月份车牌竞拍人员中,随机抽取了200人,对他们的拟报价价格进行了调查,得到如下频数分布表和频率分布直方图:

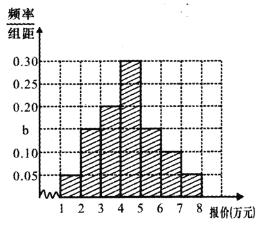
(i)求![]() 的值及这200位竟拍人员中报价大于5万元的人数;
的值及这200位竟拍人员中报价大于5万元的人数;
(ii)若2018年5月份车牌配额数量为3000,假设竞拍报价在各区间分布是均匀的,请你根据以上抽样的数据信息,预测(需说明理由)竞拍的最低成交价.
参考公式及数据:①![]() ,其中
,其中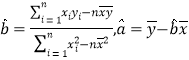 ;
;
②![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,点
上一点,点![]() 是曲线
是曲线![]() 上一点,
上一点,![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂的一个车间抽取某种产品![]() 件,产品尺寸(单位:
件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这![]() 件产品尺寸的样本平均数
件产品尺寸的样本平均数![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经过计算得
,经过计算得![]() ,利用该正态分布,求
,利用该正态分布,求![]() .
.
附:①若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】称正整数集合 A={a1,a2,…,an}(1≤a1<a2<…<an,n≥2)具有性质 P:如果对任意的i,j(1≤i≤j≤n),![]() 与
与![]() 两数中至少有一个属于A.
两数中至少有一个属于A.
(1)分别判断集合{1,3,6}与{1,3,4,12}是否具有性质 P;
(2)设正整数集合 A={a1,a2,…,an}(1≤a1<a2<…<an,n≥2)具有性质 P.证明:对任意1≤i≤n(i∈N*),ai都是an的因数;
(3)求an=30时n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() ,周长为6.
,周长为6.
(1)求椭圆![]() 的方程,并求椭圆
的方程,并求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若在
,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 与
与![]() 中点的连线与直线
中点的连线与直线![]() 垂直,求实数
垂直,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在![]() 分以下的学生后,共有男生
分以下的学生后,共有男生![]() 名,女生
名,女生![]() 名.现采用分层抽样的方法,从中抽取了
名.现采用分层抽样的方法,从中抽取了![]() 名学生,按性别分为两组,并将两组学生成绩分为
名学生,按性别分为两组,并将两组学生成绩分为![]() 组,得到如下所示频数分布表.
组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 |
|
|
|
|
|
|
女 |
|
|
|
|
|
|
(Ⅰ)规定![]() 分以上为优分(含
分以上为优分(含![]() 分),请你根据已知条件作出
分),请你根据已知条件作出![]() 列联表.
列联表.
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
合计 |
|
(Ⅱ)根据你作出的![]() 列联表判断是否有
列联表判断是否有![]() 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式:
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在![]() .
.
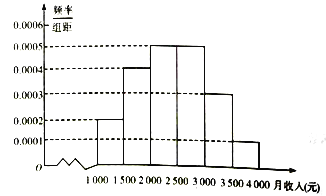
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;
(3)为了分析居民的收入与年龄、职业等方面的关系,从这10000人中用分层抽样方法抽出100人作进一步分析,则应月收入为![]() 的人中抽取多少人?
的人中抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com