
已知下列命题:
①设m为直线, 为平面,且m
为平面,且m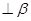 ,则“m//
,则“m// ”是“
”是“ ”的充要条件;
”的充要条件;
② 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;
③设随机变量 ~N(0,1),若P(
~N(0,1),若P( ≥2)=p,则P(-2<
≥2)=p,则P(-2< <0)=
<0)= ;
;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是( ,2);
,2);
⑤已知奇函数 满足
满足 ,且0<x<
,且0<x<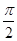 时
时 ,则函数
,则函数 在[
在[ ,
, ]上有5个零点.
]上有5个零点.
其中真命题的序号是 (写出全部真命题的序号).
③
解析试题分析:解:①因为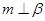 ,所以,由
,所以,由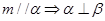 成立,
成立,
但由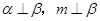 ,可得到
,可得到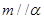 或
或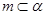 ,所以
,所以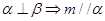 不成立,故该命题为假命題;
不成立,故该命题为假命題;
② 的展开式中第
的展开式中第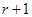 项
项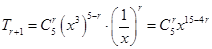 ,
,
令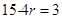 ,解得
,解得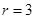 ,所以有
,所以有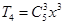 =
=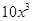 ,
, 的展开式中含x3的项的系数为10而不是60;故该命题是假命题.
的展开式中含x3的项的系数为10而不是60;故该命题是假命题.
③由随机变量 ~N(0,1),若P(
~N(0,1),若P( ≥2)=p,则
≥2)=p,则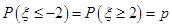 ,
,
所以,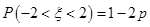
所以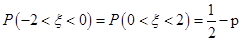 ;该命题是真命题;
;该命题是真命题;
④因为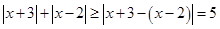
所以有,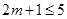 ,解得
,解得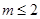
由此可知④是假命.
⑤因为奇函数 满足
满足 ,所以,
,所以,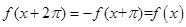 ,故函数
,故函数 是周期函数,且
是周期函数,且 ;同样由奇函数
;同样由奇函数 满足
满足 ,
,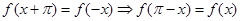
所以函数 的图象关于直线
的图象关于直线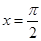 对称;
对称;
因为奇函数 满足当0<x<
满足当0<x<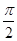 时
时 得当
得当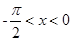 时,
时,  ,
,
又因为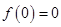
由以上条件在同一坐标系中画出函数 和
和 的图象如下图,则两图象在区间
的图象如下图,则两图象在区间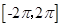 内交点的个数就是函数
内交点的个数就是函数 在区间
在区间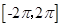 内的零点的个数;但由于
内的零点的个数;但由于 的值不能确定,故零点的个数不能确定,
的值不能确定,故零点的个数不能确定,
所以该命题是假命题.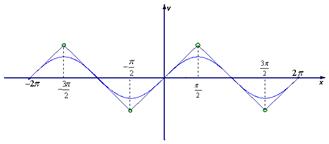
所以答案应填③
考点:1、命题;2、直线与平面的位置关系;3、二项式定理;4、正态密度曲线的性质;5、函数的性质与函数的零点.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:单选题
.(理)在正方体ABCD—A1B1C1D1中,M、N分别是棱B1C1、AD的中点,直
线AD与平面BMD1N所成角的余弦值为 ( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
命题:“若空间两条直线a,b分别垂直平面α,则a∥b”,学生小夏这样证明:
设a,b与平面α分别相交于A,B,连接AB,
∵a⊥α,b⊥α,AB?α,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,即:
①⇒②和②⇒③,老师认为小夏的推理证明不正确,这两个推理中不正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列命题:①一条直线在平面内的射影是一条直线;②在平面内射影是直线的图形一定是直线;③在同一平面内的射影长相等,则斜线长相等;④两斜线与平面所成的角相等,则这两斜线互相平行.其中真命题的个数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
α、β、γ是三个平面,a、b是两条直线,有下列三个条件:①a∥γ,b β;②a∥γ,b∥β;③b∥β,a
β;②a∥γ,b∥β;③b∥β,a γ.如果命题“α∩β=a,b
γ.如果命题“α∩β=a,b γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).
γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图所示,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com