
【题目】已知函数![]() .
.
(1)讨论![]() 的极值点的个数;
的极值点的个数;
(2)当![]() 时,若存在实数
时,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先求得函数![]() 的导函数
的导函数![]() .令
.令![]() ,分离参数后构造函数
,分离参数后构造函数![]() ,并求得
,并求得![]() ,通过判断
,通过判断![]() 在各区间内的符号,判断
在各区间内的符号,判断![]() 的单调性及
的单调性及![]() 的取值情况.即可根据
的取值情况.即可根据![]() 的取值情况,判断极值点的个数.
的取值情况,判断极值点的个数.
(2)将![]() 代入,并令
代入,并令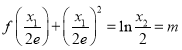 ,即可用
,即可用![]() 表示出
表示出![]() 与
与![]() ,即可表示出
,即可表示出![]() .构造函数
.构造函数![]() ,并求得
,并求得![]() ,结合
,结合![]() 的符号即可判断
的符号即可判断![]() 的单调性,进而求得
的单调性,进而求得![]() 的最小值.
的最小值.
(1)由题可知![]() ,
,
令![]() ,得
,得![]() ,
,
记![]() ,则
,则![]()
当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]()
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ,
,
∴当![]() 时,函数
时,函数![]() 有2个极值点;
有2个极值点;
当![]() 时,函数
时,函数![]() 无极值点;
无极值点;
当![]() 时,函数
时,函数![]() 有1个极值点;
有1个极值点;
(2)当![]() 时,设
时,设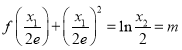 ,
,
则![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
故![]() ,
,![]() ,
,
∴![]() ,
,![]() ,即
,即![]() .
.
令![]() ,
,
则![]() ,
,
∵![]() 与
与![]() 在
在![]() 均单调递增,
均单调递增,
∴![]() 在
在![]() 均单调递增,且
均单调递增,且![]() ,
,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: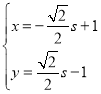 (
(![]() 为参数),以O为极点,
为参数),以O为极点,![]() 轴的非负半轴为极轴的极坐标系中,已知曲线
轴的非负半轴为极轴的极坐标系中,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记曲线
,记曲线![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的极坐标;
的极坐标;
(2)设曲线![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点,给出命题:①
的零点,给出命题:①![]() ;②若
;②若![]() ,则存在
,则存在![]() ,使得
,使得![]() ;③
;③![]() 与
与![]() 所有极值之和一定小于0;④若
所有极值之和一定小于0;④若![]() ,且
,且![]() 是曲线
是曲线![]() 的一条切线,则
的一条切线,则![]() 的取值范围是
的取值范围是![]() .则以上命题正确序号是_____________.
.则以上命题正确序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
(1)当![]() ,
,![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)若对于任何实数![]() ,函数
,函数![]() 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的图象上
的图象上![]() 、
、![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且直线
的不动点,且直线![]() 是线段
是线段![]() 的垂直平分线,求实数
的垂直平分线,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界排球比赛一般实行“五局三胜制”,在2019年第13届世界女排俱乐部锦标赛(俗称世俱杯)中,中国女排和某国女排相遇,根据历年数据统计可知,在中国女排和该国女排的比赛中,每场比赛中国女排获胜的概率为![]() ,该国女排获胜的概率为
,该国女排获胜的概率为![]() ,现中国女排在先胜一局的情况下获胜的概率为( )
,现中国女排在先胜一局的情况下获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为30°的直线,交
夹角为30°的直线,交![]() 于点
于点![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知A,B分别为椭圆C:![]() (a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,
(a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,![]()
![]() =﹣4,△PAB的面积的最大值为
=﹣4,△PAB的面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)若椭圆C上存在两点M,N,分别满足OM∥PA,ON∥PB,求|OM||ON|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线l与椭圆C交于P,Q两点,且点M满足
,直线l与椭圆C交于P,Q两点,且点M满足![]() .
.
(1)若点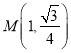 ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线l过点![]() 且不与x轴重合,过点M作垂直于l的直线
且不与x轴重合,过点M作垂直于l的直线![]() 与y轴交于点
与y轴交于点![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com