
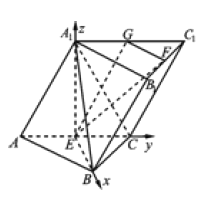
【题目】如图,在三棱柱中![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
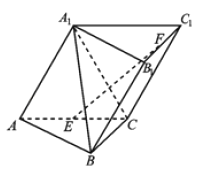
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,根据线线平行证线面平行,再根据线面平行得面面平行,最后根据面面平行得结果,(2)先根据条件得
,根据线线平行证线面平行,再根据线面平行得面面平行,最后根据面面平行得结果,(2)先根据条件得![]() ,
,![]() ,
,![]() 两两垂直,再建立空间直角坐标系,设各点坐标,利用方程组解得各面法向量,再根据向量数量积得法向量夹角,最后根据二面角与法向量夹角关系得结果.
两两垂直,再建立空间直角坐标系,设各点坐标,利用方程组解得各面法向量,再根据向量数量积得法向量夹角,最后根据二面角与法向量夹角关系得结果.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由于
,由于![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .又
.又![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形.
是平行四边形.
则![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以平面![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]()
(2)解:令![]() ,
,
由于![]() 为
为![]() 中点,则
中点,则![]() ,又侧面
,又侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,
,![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,连接
,连接![]() ,可知
,可知![]() ,
,![]() ,
,![]() 两两垂直.以
两两垂直.以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
令平面![]() 的法向量为
的法向量为![]() ,
,
由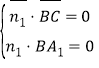 则
则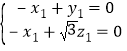 令
令![]() ,则
,则![]() .
.
令平面![]() 的法向量为
的法向量为![]() ,
,
由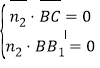 则
则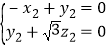 令
令![]() ,则
,则![]()
由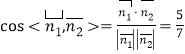 ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
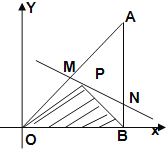
【题目】如图所示,将一块直角三角形板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角板锯成
将三角板锯成![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
(1)用![]() 表示出直线
表示出直线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标;
的坐标;
(2)求出![]() 的取值范围及其所对应的倾斜角
的取值范围及其所对应的倾斜角![]() 的范围;
的范围;
(3)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,![]() 为坐标原点,射线
为坐标原点,射线![]() 与
与![]() 轴正半轴重合,射线
轴正半轴重合,射线![]() 在第一象限,且与
在第一象限,且与![]() 轴正半轴的夹角为
轴正半轴的夹角为![]() ,在
,在![]() 上有点列
上有点列![]() ,在
,在![]() 上有点
上有点![]() ,已知
,已知![]() ,
,![]()
(1)求点![]() 和
和![]() 的坐标;
的坐标;
(2)求![]() 的坐标;
的坐标;
(3)求![]() 面积的最大值,并求出此时的
面积的最大值,并求出此时的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个生产公司投资A生产线500万元,每万元可创造利润![]() 万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了
万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了![]() ;若将少用的x万元全部投入B生产线,每万元创造的利润为
;若将少用的x万元全部投入B生产线,每万元创造的利润为![]() 万元,其中
万元,其中![]() .
.
![]() 若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
![]() 若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的任一条直线
的任一条直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元![]() 今年,工厂第一次投入100万元
今年,工厂第一次投入100万元![]() 科技成本
科技成本![]() ,并计划以后每年比上一年多投入100万元
,并计划以后每年比上一年多投入100万元![]() 科技成本
科技成本![]() ,预计产量年递增10万只,第
,预计产量年递增10万只,第![]() 次投入后,每只产品的固定成本为
次投入后,每只产品的固定成本为![]() 为常数,
为常数,![]() 且
且![]() ,若产品销售价保持不变,第
,若产品销售价保持不变,第![]() 次投入后的年利润为
次投入后的年利润为![]() 万元.
万元.
(1)求![]() 的值,并求出
的值,并求出![]() 的表达式;
的表达式;
(2)问从今年算起第几年利润最高?最高利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com