
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)对于任意![]() 且
且![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析(2)![]()
【解析】
(1)对f(x)求导,分![]() 和
和![]() ,确定导函数的正负,从而判断函数的单调性;
,确定导函数的正负,从而判断函数的单调性;
(2)由题意原不等式可变形为![]() 恒成立,构造函数
恒成立,构造函数![]() ,原题转化为
,原题转化为![]() 在
在![]() 上为单调增函数,即
上为单调增函数,即![]() 对
对![]() 恒成立,分离参数得到
恒成立,分离参数得到![]() ,利用导数研究不等式右边函数的最值即可.
,利用导数研究不等式右边函数的最值即可.
(1)![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上为单调增函数;
上为单调增函数;
当![]() 时,
时,![]() 在
在![]() 上有
上有![]() ,
,![]() 在
在![]() 为单调减函数;
为单调减函数;![]() 在
在![]() 上有
上有![]() ,
,![]() 在
在![]() 为单调增函数.
为单调增函数.
综上所述:当![]() 时,
时,![]() 在
在![]() 上为单调增函数;
上为单调增函数;
当![]() 时,
时,![]() 在
在![]() 为单调减函数,
为单调减函数,![]() 在
在![]() 为单调增函数.
为单调增函数.
(2)∵![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立,
令![]()
题意即为![]() 恒成立,而
恒成立,而![]() ,
,
故上述不等式转化为![]() 在
在![]() 上为单调增函数,
上为单调增函数,
即![]() 对
对![]() 恒成立;
恒成立;
![]() ,
,
题意即为不等式![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
则![]()
令![]() ,
,![]()
![]() ,
,![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ;
;
于是![]() 在
在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() ,
,
即函数![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
所以![]() 在
在![]() 处取得最小值,
处取得最小值,![]()
因此![]() ,故实数
,故实数![]() 的范围为
的范围为![]()


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某支教队有8名老师,现欲从中随机选出2名老师参加志愿活动,
(1)若规定选出的至少有一名女老师,则共有18种不同的需安排方案,试求该支教队男、女老师的人数;
(2)在(1)的条件下,记![]() 为选出的2位老师中女老师的人数,写出
为选出的2位老师中女老师的人数,写出![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品.
内的产品为合格品,否则为不合格品.
注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量(克) | 频数 |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
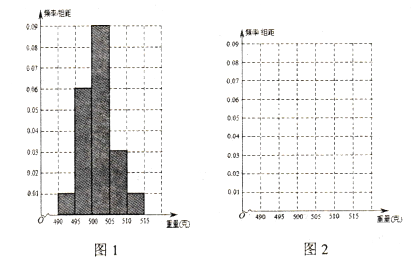
(1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
甲流水线 | 乙流水线 | 合计 | |
合格 | |||
不合格 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上任意一点
上任意一点![]() 到直线
到直线![]() 的距离是它到点
的距离是它到点![]() 距离的2倍;曲线
距离的2倍;曲线![]() 是以原点为顶点,
是以原点为顶点,![]() 为焦点的抛物线.
为焦点的抛物线.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() 两点,分别以
两点,分别以![]() 为切点引曲线
为切点引曲线![]() 的两条切线
的两条切线![]() ,设
,设![]() 相交于点
相交于点![]() ,连接
,连接![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com