练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若f(x)＝f1(x)＝，fn(x)＝fn－1[f(x)](n≥2，n∈N*)，则f(1)＋f(2)＋…＋f(n)＋f1(1)＋f2(1)＋…＋fn(1)＝

    A.n             B.             C.             D.1

     

    【答案】

    A

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2008年普通高等学校招生全国统一考试(江苏卷)、数学 题型：044

    若，，x∈R，p1，p2为常数，且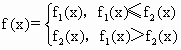

    (1)求f(x)＝f1(x)对所有实数x成立的充要条件(用p1，p2表示)

    (2)设a，b为两实数，a＜b且p1，p2∈(a，b)若f(a)＝f(b)

    求证：f(x)在区间[a，b]上的单调增区间的长度和为(闭区间[m，n]的长度定义为n－m)

    查看答案和解析>>

    科目：高中数学 来源：江西省临川一中、新余四中2012届高三上学期期中考试数学理科试题 题型：044

    已知函数．

    (1)若a＝2，求f(x)＝f1(x)＋f2(x)在x±[2，3]上的最小值；

    (2)当4≤a≤6时，求函数在x∈[1，6]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源：山东省莱州一中2012届高三第二次质量检测数学理科试题 题型：044

    若函数f(x)＝sin2x＋2cos2x＋m在区间[0，]上的最大值为6，

    (1)求常数m的值

    (2)作函数f(x)关于y轴的对称图象得函数f1(x)的图象，再把f1(x)的图象向右平移个单位得f2(x)的图象，求函数f2(x)的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝ax2＋ln x(a∈R)

    (Ⅰ)当a＝2时，求f(x)在区间[e，e2]上的最大值和最小值；

    (Ⅱ)如果函数g(x)，f1(x)，f2(x)在公共定义域D上，满足f1(x)<g(x)<f2(x)，那么就称g(x)为f1(x)，f2(x)的“伴随函数”.已知函数f1(x)＝x2＋2ax＋(1－a2)ln x，f2(x)＝x2＋2ax.若在区间(1，＋∞)上，函数f(x)是f1(x)，f2(x)的“伴随函数”，求a的取值范围.

    查看答案和解析>>

    同步练习册答案