解析:∵(1+2x-3x2)6=(3x2-2x-1)6=[(x-1)(3x+1)]6=(x-1)6(3x+1)6,
而(1+3x)6的通项为Tk+1=3k·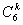 ·xk,
·xk,
(x-1)6=(1-x)6的通项为Tr+1=(-1)r·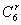 ·xr,
·xr,
∴(x-1)6(3x+1)6的通项为(-1)r·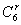 ·3k·
·3k·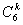 ·xr+k.
·xr+k.
令r+k=5且k∈{0,1,2,3,4,5,6},r∈{0,1,2,3,4,5,6},
∴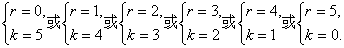
故所求的项为
[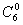 ·35·
·35·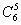 +(-1)1·
+(-1)1·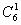 ·34·
·34·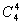 +(-1)2·
+(-1)2·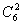 ·33·
·33·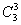 +(-1)3·
+(-1)3· ·32·
·32·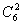 +(-1)4·
+(-1)4·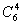 ·31·
·31·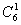 +(-1)5·
+(-1)5·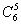 ·30·
·30·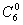 ]x5=-168x5.
]x5=-168x5.

 阅读快车系列答案
阅读快车系列答案