
����Ŀ��![]() ָ���������ع�������������������ƽ���ó������֣��ǹ����ϳ��õĺ����������ݳ̶��Լ��Ƿ���һ���������ڸ����������س������ԣ���
ָ���������ع�������������������ƽ���ó������֣��ǹ����ϳ��õĺ����������ݳ̶��Լ��Ƿ���һ���������ڸ����������س������ԣ���![]() ��ֵ���ڻ����20.5ʱ������˵���ؽ��أ���
��ֵ���ڻ����20.5ʱ������˵���ؽ��أ���![]() ��ֵС��20.5ʱ������˵���ؽ��ᣬ���ߴ��ڻ����
��ֵС��20.5ʱ������˵���ؽ��ᣬ���ߴ��ڻ����![]() ����˵���߽ϸߣ�����С��170cm����˵���߽ϰ���
����˵���߽ϸߣ�����С��170cm����˵���߽ϰ���
������֪ij���й���32���������س�������������![]() ָ����������ɢ��ͼ�������������Ϣ��������������������ж��Ƿ���
ָ����������ɢ��ͼ�������������Ϣ��������������������ж��Ƿ���![]() �İ�����Ϊ���������߶�
�İ�����Ϊ���������߶�![]() ָ����Ӱ�죮
ָ����Ӱ�죮

���߽ϰ� | ���߽ϸ� | �ϼ� | |
���ؽ��� | |||
���ؽ��� | |||
�ϼ� |
���ٴ�����32���������س��������ѡȡ8���������ߺ����ص����������ʾ��
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
���� | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
���� | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
������С���˷���˼���빫ʽ������Իع鷽��Ϊ![]() �������Ѿ���õ����Իع鷽�̣����������вв��������
�������Ѿ���õ����Իع鷽�̣����������вв��������![]() �����ͱ��������ߣ�����Ԥ�����������أ��仯�Ĺ���ֵ����������λ��Ч���֣���
�����ͱ��������ߣ�����Ԥ�����������أ��仯�Ĺ���ֵ����������λ��Ч���֣���
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
���أ�kg�� | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
�в� |
|
|
|
|
|
|
|
��ͨ���в���������ڲв�������ֵ�����������ݣ���Ҫȷ����������IJɼ����Ƿ�����Ϊ�Ĵ�����֪ͨ�����²ɼ����֣��������ݵ�����Ӧ��Ϊ![]() ��С�����¸�����С���˷���˼���빫ʽ�������
��С�����¸�����С���˷���˼���빫ʽ�������![]() ������С������Ļ���������������س��������������ص����Իع鷽�̣�
������С������Ļ���������������س��������������ص����Իع鷽�̣�
�ο����ݣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ο���ʽ��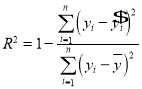 ��
��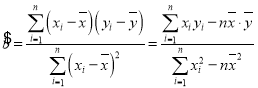 ��
��![]() ��
��![]() ��
��![]() ��
��
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
���𰸡��������������������û��![]() �İ�����Ϊ���������߶�
�İ�����Ϊ���������߶�![]() ָ����Ӱ�죻�������в�����������
ָ����Ӱ�죻�������в�����������![]() ԼΪ0.91����
ԼΪ0.91����![]() ��
��
��������
������ɢ��ͼ���������������![]() ����ж�Ӧ�ٽ�ֵ�Ƚϼ����жϣ�����������Ϊ8�����ݵIJв��Ӧֵ���빫ʽ
����ж�Ӧ�ٽ�ֵ�Ƚϼ����жϣ�����������Ϊ8�����ݵIJв��Ӧֵ���빫ʽ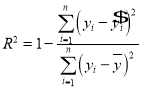 ���㼴�ɣ������
���㼴�ɣ������![]() ������
������![]() ������
�м������![]() ���Ӷ���ûع鷽��.
���Ӷ���ûع鷽��.
����
���߽ϰ� | ���߽ϸ� | �ϼ� | |
���ؽ��� | 6 | 15 | 21 |
���ؽ��� | 6 | 5 | 11 |
�ϼ� | 12 | 20 | 32 |
����![]() ��
��
���û��![]() �İ�����Ϊ���������߶�
�İ�����Ϊ���������߶�![]() ָ����Ӱ�죮
ָ����Ӱ�죮
�������Ա��Ϊ8������![]() ����ɲв��������ʾ��
����ɲв��������ʾ��
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
���� | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
�в� | 0.1 | 0.3 | 0.9 |
|
|
|
| 3.5 |
![]()
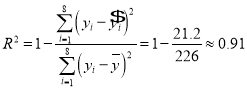 ��
��
���Խ��ͱ��������ߣ�����Ԥ�����������أ��仯�Ĺ���ֵ![]() ԼΪ0.91��
ԼΪ0.91��
��������֪���ڰ������ݵ�����ӦΪ58����ʱ����֪��![]() ��
��![]() ��
��
![]() ��
��
�������²ɼ����ݺ��������س��������������ص����Իع鷽��Ϊ![]() ��
��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����|2x��1|��3|x+1|����f��x�������ֵΪM.
��1����M��
��2��������a��b����![]() Mab��֤����a4b+ab4
Mab��֤����a4b+ab4![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�Ķ�����ABCDEF���㣺������ABCD����������FBC���ڵ�����ƽ�滥�ഹֱ��FB��AE��FB��2EA.
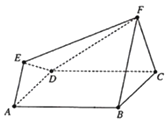
��1��֤����ƽ��EFD��ƽ��ABFE��
��2��������E��FD��C������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ��
��![]() ��һ�㣮
��һ�㣮
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() ��
��![]() �ֱ�����������ἰ����ԭ��ĶԳƵ㣬ƽ����
�ֱ�����������ἰ����ԭ��ĶԳƵ㣬ƽ����![]() ��ֱ��
��ֱ��![]() ��
��![]() ������
������![]() ������
������![]() ����
����![]() ����ԭ��ĶԳƵ�Ϊ
����ԭ��ĶԳƵ�Ϊ![]() ��֤����ֱ��
��֤����ֱ��![]() ��
��![]() ��Χ�ɵ��������ǵ��������Σ�
��Χ�ɵ��������ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ���϶���Ϊ
���϶���Ϊ![]() ��ֱ��
��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ����ԭ�㵽ֱ��
����ԭ�㵽ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() .
.
��1������Բ![]() �ı����̣�
�ı����̣�
��2������������![]() ��ֱ��
��ֱ��![]() ��
��![]() ����Բ
����Բ![]() ����
����![]() ���㣬����Բ
���㣬����Բ![]() ����.��̽��
����.��̽��![]() ���ܳ��Ƿ�Ϊ��ֵ�����ǣ������ֵ�������ǣ���˵������.
���ܳ��Ƿ�Ϊ��ֵ�����ǣ������ֵ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ��
��![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������![]() ��������ͬ�����
��������ͬ�����![]() .
.
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��������֤��![]() .������
.������![]() Ϊ
Ϊ![]() �ļ�Сֵ�㣩
�ļ�Сֵ�㣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ���¹ڷ��������ڼ䣬�ҹ�ҽ������������ҵ�Ӱ�ӵ��������֡�������������ˮ�ȷ�����Ʒ�����Ͽ���һ��ҽ�����ʹ�Ӧ���ڹ��������Ӯ��һƬ����.�ҹ�ij����������ҵ�ڼӴ�������ͬʱ����ץ��������������ʱ����������������ҵ�ʼ���Ա���������Ŀ����������ȡ��100������������ָ��ֵ�ֳ��������飺![]() ��
��![]() ��
��![]() ������
������![]() ���õ�����Ƶ�ʷֲ�ֱ��ͼ.
���õ�����Ƶ�ʷֲ�ֱ��ͼ.
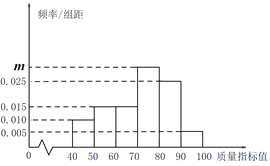
��1�����ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2�������������������˼�룬���Ƹ���ҵ�������Ŀ��ֵ�����ָ��ֵ��ƽ��������λ����ͬһ���е������ø��������е�ֵ����������λ����ȷ��0.01����
��3���ֹ涨������ָ��ֵС��70�Ŀ���Ϊ����Ʒ������ָ��ֵ��С��70�Ŀ���Ϊһ��Ʒ.���÷ֲ�����ķ����Ӹ���ҵ����ȡ��100�������г��5�����֣��������������ȡ2������һ��������������������2��������ǡ����1������Ϊһ��Ʒ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ����У���������ļ��㹫ʽΪ![]() ������
������![]() ��
Ϊ��![]() ����Ѷȣ�
����Ѷȣ� ![]() Ϊ��Ը����������
Ϊ��Ը���������� ![]() Ϊ�μӲ��Ե�������.�ֶ�ijУ�����꼶120��ѧ������һ�β��ԣ���5������.����ǰ���ݶ�ѧ�����˽⣬Ԥ����ÿ������Ѷȣ����±���ʾ��
Ϊ�μӲ��Ե�������.�ֶ�ijУ�����꼶120��ѧ������һ�β��ԣ���5������.����ǰ���ݶ�ѧ�����˽⣬Ԥ����ÿ������Ѷȣ����±���ʾ��

���Ժ��������ȡ��10��ѧ���������DZ�ź�ͳ�Ƹ����������������±���ʾ�����̡���ʾ��ԣ���������ʾ�������
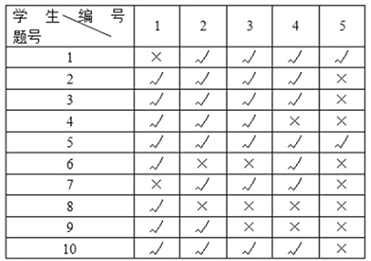
��1�������������ݣ���������10��ѧ��ÿ����ʵ��Ĵ����������Ӧ��ʵ���Ѷ������±�����������120��ѧ���е�5���ʵ����������

��2���ӱ��Ϊ1��5��5���������ȡ2�ˣ���ǡ����1�˴�Ե�5��ĸ��ʣ�
��3������ͳ����![]() ������
������![]() ��
Ϊ��![]() ���ʵ���Ѷȣ�
���ʵ���Ѷȣ� ![]() Ϊ��
Ϊ��![]() ���Ԥ���Ѷȣ�
���Ԥ���Ѷȣ�![]() ��.�涨����
��.�涨����![]() ����Ƹôβ��Ե��Ѷ�Ԥ������������Ϊ������.�жϱ��β��Ե��Ѷ�Ԥ���Ƿ����.
����Ƹôβ��Ե��Ѷ�Ԥ������������Ϊ������.�жϱ��β��Ե��Ѷ�Ԥ���Ƿ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڸ�һ�꼶һ������������������Ż������ȵ��飨���ֻ�������������������������֣����ӱ������ѧ���������ȡ��50�ˣ�����ĵ����������
��� | һ�� | ���� | ���� | �İ� | ��� | ���� |
Ƶ�� | 4 | 5 | 11 | 8 | 10 | 12 |
�������� | 3 | 2 | 8 | 5 | 6 | 6 |
�ִ�һ��Ͷ��������������ѡȡ4�˽����ٵ��飬��ѡ�е�4����ǡ��2�˲�����ĸ���Ϊ___________����������ͳ��������ѧ��������̬�ȵ�Ƶ����Ϊ���ʣ��ڸ�һ�꼶ȫ��ѧ���������ȡ3��ѧ�������������������ΪX�����������X����ѧ������___________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com