
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, ![]() )的部分图象如图所示.
)的部分图象如图所示. 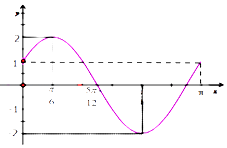
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间和对称中心.
【答案】
(1)解:显然A=2,又图象过(0,1)点,∴f(0)=1,
∴sin φ= ![]() ,∵|φ|<
,∵|φ|< ![]() ,∴φ=
,∴φ= ![]() ;
;
由图象结合“五点法”可知ω ![]() +
+ ![]() =2π,得ω=2.
=2π,得ω=2.
所以所求的函数的解析式为:f(x)=2sin(2x+ ![]() ).
).
(2)解:﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,可得函数f(x)的单调递增区间[﹣
+2kπ,可得函数f(x)的单调递增区间[﹣ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z);
+kπ](k∈Z);
令 ![]() ,
, ![]() ,对称中心
,对称中心 ![]()
【解析】(1)利用最值求出A,利用周期求出ω,利用特殊点,求出φ,即可求函数f(x)的解析式;(2)利用正弦函数的性质,求函数f(x)的单调递增区间和对称中心.
【考点精析】本题主要考查了正弦函数的单调性的相关知识点,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能正确解答此题.
上是减函数才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(I)求证:直线![]() 平面
平面![]() .
.
(II)求证:直线![]() 平面
平面![]() .
.
(III)在![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
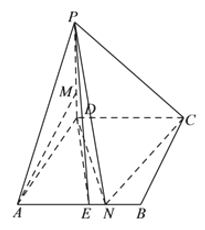
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0, ![]() )上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
A.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)![]()
B.f(1)<2f( ![]() )sin1
)sin1
C.![]() f(
f( ![]() )>f(
)>f( ![]() )
)![]()
D.![]() f(
f( ![]() )<f(
)<f( ![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,以A为圆心,AD为半径的圆交AC,AB于M,E.CE的延长线交⊙A于F,CM=2,AB=4.
(1)求⊙A的半径;
(2)求CE的长和△AFC的面积
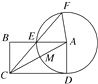
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=﹣tan2x,有下列说法: ①f(x)的定义域是{x∈R|x≠ ![]() +kπ,k∈Z}②f(x)是奇函数 ③在定义域上是增函数 ④在每一个区间(﹣
+kπ,k∈Z}②f(x)是奇函数 ③在定义域上是增函数 ④在每一个区间(﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() )(k∈Z)上是减函数 ⑤最小正周期是π其中正确的是( )
)(k∈Z)上是减函数 ⑤最小正周期是π其中正确的是( )
A.①②③
B.②④⑤
C.②④
D.③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足: ![]() 和
和![]() ,则称直线
,则称直线![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
, ![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的极值;
的极值;
(2)函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】兰州一中在世界读书日期间开展了“书香校园”系列读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”。
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 |
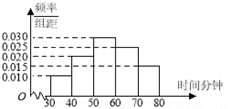
(1)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(2)利用分层抽样从这100名学生的“读书迷”中抽取8名进行集训,从中选派2名参加兰州市读书知识比赛,求至少有一名男生参加比赛的概率。
附: 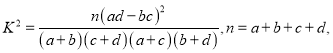
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com