
【题目】如图,在矩形ABCD中,以A为圆心,AD为半径的圆交AC,AB于M,E.CE的延长线交⊙A于F,CM=2,AB=4.
(1)求⊙A的半径;
(2)求CE的长和△AFC的面积
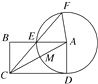
【答案】(1)3(2) ![]()
【解析】试题分析:(1)根据勾股定理得关于半径关系式,解得半径;(2)由直角三角形可得CE的长,由切割线定理可得CF,根据解三角形可得三角形面积
试题解析:解:(1)∵四边形ABCD为矩形,AB=4,∴CD=4.
在Rt△ACD中,AC2=CD2+AD2,
∴(2+AD)2=42+AD2.
解得:AD=3,即⊙A的半径为3.
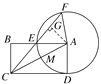 (2)过点A作AG⊥EF于点G,
(2)过点A作AG⊥EF于点G,
∵BC=3,
BE=AB-AE=4-3=1,
∴CE=![]()
=![]() =
=![]() .
.
∵∠ADC=90°,
∴CD为⊙A的切线,
∴CE·CF=CD2,
∴CF=![]() =
=![]() =
=![]()
![]() .
.
又∠B=∠AGE=90°,∠BEC=∠GEA,
∴△BCE∽△GAE,
∴![]() =
=![]() 即
即![]() =
=![]() .∴AG=
.∴AG=![]()
![]() ,
,
∴S△AFC=![]() CF·AG=
CF·AG=![]() ×
×![]()
![]() ×
×![]()
![]() =
=![]() .
.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域是D,若存在常数m、M,使得m≤f(x)≤M对任意x∈D成立,则称函数f(x)是D上的有界函数,其中m称为函数f(x)的下界,M称为函数f(x)的上界;特别地,若“=”成立,则m称为函数f(x)的下确界,M称为函数f(x)的上确界. (Ⅰ)判断 ![]() 是否是有界函数?说明理由;
是否是有界函数?说明理由;
(Ⅱ)若函数f(x)=1+a2x+4x(x∈(﹣∞,0))是以﹣3为下界、3为上界的有界函数,求实数a的取值范围;
(Ⅲ)若函数 ![]() ,T(a)是f(x)的上确界,求T(a)的取值范围.
,T(a)是f(x)的上确界,求T(a)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() cos(2x﹣
cos(2x﹣ ![]() ).
).
(1)若sinθ=﹣ ![]() ,θ∈(
,θ∈( ![]() ,2π),求f(θ+
,2π),求f(θ+ ![]() )的值;
)的值;
(2)若x∈[ ![]() ,
, ![]() ],求函数f(x)的单调减区间.
],求函数f(x)的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对任意平面向量 ![]() =(x,y),把
=(x,y),把 ![]() 绕其起点沿逆时针方向旋转θ角得到的向量
绕其起点沿逆时针方向旋转θ角得到的向量 ![]() =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
=(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
(1)已知平面内点A(2,3),点B(2+2 ![]() ,1).把点B绕点A逆时针方向旋转
,1).把点B绕点A逆时针方向旋转 ![]() 角得到点P,求点P的坐标.
角得到点P,求点P的坐标.
(2)设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转 ![]() 后得到的点的轨迹方程是曲线y=
后得到的点的轨迹方程是曲线y= ![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1=2x+1+(x2﹣3x+2)i,z2=x2﹣2+(x2+x﹣6)i(x∈R).
(1)若z1是纯虚数,求实数x的取值范围;
(2)若z1>z2 , 求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, ![]() )的部分图象如图所示.
)的部分图象如图所示. 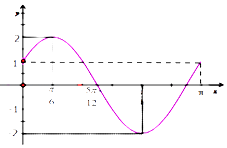
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com