
【题目】定义:若函数![]() 的定义域为
的定义域为![]() ,且存在非零常数
,且存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() 恒成立,则称
恒成立,则称![]() 为线周期函数,
为线周期函数, ![]() 为
为![]() 的线周期.
的线周期.
(Ⅰ)下列函数①![]() ,②
,②![]() ,③
,③![]() (其中
(其中![]() 表示不超过
表示不超过![]() 的最大整数),是线周期函数的是(直接填写序号);
的最大整数),是线周期函数的是(直接填写序号);
(Ⅱ)若![]() 为线周期函数,其线周期为
为线周期函数,其线周期为![]() ,求证:函数
,求证:函数![]() 为周期函数;
为周期函数;
(Ⅲ)若![]() 为线周期函数,求
为线周期函数,求![]() 的值.
的值.
【答案】(1) ③(2)见解析(3) ![]()
【解析】试题分析:(Ⅰ)根据新定义逐个判断即可;
(Ⅱ)根据新定义证明出![]()
![]() ,即可证得函数
,即可证得函数![]() 为周期函数;
为周期函数;
(Ⅲ)φ(x)=sinx+kx为线周期函数,可得存在非零常数T,对任意x∈R,sin(x+T)+k(x+T)=sinx+kx+T.即可得到2kT=2T,解得验证即可.
试题解析:
(Ⅰ)对于①f(x+T)=2x+T=2x2T=f(x)2T,故不是线周期函数
对于②f(x+T)=log2(x+T)≠f(x)+T,故不是线周期函数
对于③f(x+T)=[x+T]=[x]+T=f(x)+T,故是线周期函数
故答案为③
(Ⅱ)证明:∵![]() 为线周期函数,其线周期为
为线周期函数,其线周期为![]() ,
,
∴存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() 恒成立.
恒成立.
∵![]() ,
,
∴![]()
![]() .
.
∴![]() 为周期函数.
为周期函数.
(Ⅲ)∵![]() 为线周期函数,
为线周期函数,
∴存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() .
.
∴![]() .
.
令![]() ,得
,得![]() ;…………①
;…………①
令![]() ,得
,得![]() ;…………②
;…………②
①②两式相加,得![]() .
.
∵![]() ,
,
∴![]() .
.
检验:
当![]() 时,
时, ![]() .
.
存在非零常数![]() ,对任意
,对任意![]() ,
,
![]()
![]() ,
,
∴![]() 为线周期函数.
为线周期函数.
综上, ![]() .
.


科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟) 变化的函数关系式近似为
(分钟) 变化的函数关系式近似为![]() ,其中
,其中 .根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若投放![]() 个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求
个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求![]() 的值;
的值;
(2)若投放4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的右焦点与抛物线y2=4x的焦点重合,点M ![]() 在椭圆E上. (Ⅰ)求椭圆E的标准方程;
在椭圆E上. (Ⅰ)求椭圆E的标准方程;
(Ⅱ)设P(﹣4,0),直线y=kx+1与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b. (0 <φ < π)
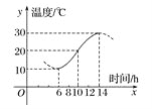
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足:
满足: ![]() ,且该函数的最小值为1.
,且该函数的最小值为1.
(1)求此二次函数![]() 的解析式;
的解析式;
(2)若函数![]() 的定义域为
的定义域为![]() (其中
(其中![]() ),问是否存在这样的两个实数
),问是否存在这样的两个实数![]() ,
, ![]() ,使得函数
,使得函数![]() 的值域也为
的值域也为![]() ?若存在,求出
?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若对于任意的![]() ,总存在
,总存在![]() 使得
使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资、薪金(扣除三险一金后)所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额个人所得税计算公式:应纳税额=工资-三险一金=起征点. 其中,三险一金标准是养老保险8%、医疗保险2%、失业保险1%、住房公积金8%,此项税款按下表分段累计计算:
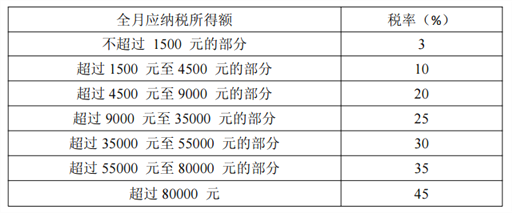
(1)某人月收入15000元(未扣三险一金),他应交个人所得税多少元?
(2)某人一月份已交此项税款为1094元,那么他当月的工资(未扣三险一金)所得是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象,若函数g(x)在区间[0,
)个单位后得到函数g(x)的图象,若函数g(x)在区间[0, ![]() ]上单调递增,则φ的取值范围是( )
]上单调递增,则φ的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 是定义在实数集
是定义在实数集![]() 上的奇函数,并且在区间
上的奇函数,并且在区间![]() 上是单调递增的函数.
上是单调递增的函数.
(1)研究并证明函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)若实数![]() 满足不等式
满足不等式![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com