
【题目】已知二次函数![]() 满足:
满足: ![]() ,且该函数的最小值为1.
,且该函数的最小值为1.
(1)求此二次函数![]() 的解析式;
的解析式;
(2)若函数![]() 的定义域为
的定义域为![]() (其中
(其中![]() ),问是否存在这样的两个实数
),问是否存在这样的两个实数![]() ,
, ![]() ,使得函数
,使得函数![]() 的值域也为
的值域也为![]() ?若存在,求出
?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若对于任意的![]() ,总存在
,总存在![]() 使得
使得![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2) 存在满足条件的
(2) 存在满足条件的![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() (3)
(3)![]()
【解析】试题分析: ![]() 设
设![]() ,由
,由![]() ,求出
,求出![]() 的值,可得此二次函数
的值,可得此二次函数![]() 的解析式;
的解析式;
![]() 分
分![]() 时,当
时,当![]() 时,当
时,当![]() 时,三种情况讨论,可得满足条件的
时,三种情况讨论,可得满足条件的![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ;
;
![]() 若对于任意的
若对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,进而得到答案;
,进而得到答案;
解析:(1)依题意,可设![]() ,因
,因![]() ,代入得
,代入得![]() ,所以
,所以![]() .
.
(2)假设存在这样的![]() ,
, ![]() ,分类讨论如下:
,分类讨论如下:
当![]() 时,依题意,
时,依题意, 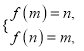 即
即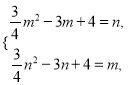 两式相减,整理得
两式相减,整理得
![]() ,代入进一步得
,代入进一步得![]() ,产生矛盾,故舍去;
,产生矛盾,故舍去;
当![]() 时,依题意
时,依题意![]() ,
,
若![]() ,
, ![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
若![]() ,
, ![]() ,产生矛盾,故舍去;
,产生矛盾,故舍去;
当![]() 时,依题意,
时,依题意, 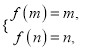 即
即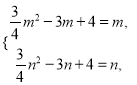 解得
解得![]() ,
, ![]() 产生矛盾,故舍去.
产生矛盾,故舍去.
综上:存在满足条件的![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() .
.
(3)依题意: ![]() ,
,
由(1)可知, ![]() ,
, ![]() ,
,
即![]() 在
在![]() 上有解;
上有解;
整理得![]() ,
, ![]() 有解,
有解,
又![]()
![]() ,
, ![]() ,当
,当![]() 时,有
时,有![]() ;
;
依题意: ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求实数m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并说明理由;
(3)当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞),求实数n,a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() 为
为![]() 中点.
中点.
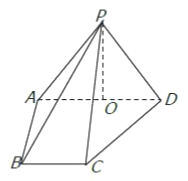
(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)线段![]() 上是否存在
上是否存在![]() ,使得它到平面
,使得它到平面![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在发展过程中,交通状况逐渐受到有关部门的关注,据有关统计数据显示,从上午6点到中午12点,车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出: y= 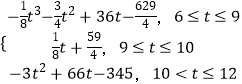
求从上午6点到中午12点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的定义域为
的定义域为![]() ,且存在非零常数
,且存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() 恒成立,则称
恒成立,则称![]() 为线周期函数,
为线周期函数, ![]() 为
为![]() 的线周期.
的线周期.
(Ⅰ)下列函数①![]() ,②
,②![]() ,③
,③![]() (其中
(其中![]() 表示不超过
表示不超过![]() 的最大整数),是线周期函数的是(直接填写序号);
的最大整数),是线周期函数的是(直接填写序号);
(Ⅱ)若![]() 为线周期函数,其线周期为
为线周期函数,其线周期为![]() ,求证:函数
,求证:函数![]() 为周期函数;
为周期函数;
(Ⅲ)若![]() 为线周期函数,求
为线周期函数,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣4x,g(x)=﹣x2﹣3. (Ⅰ)求函数f(x)在x=1处的切线方程;
(Ⅱ)若存在x0∈[e,e2],使得f(x0)<g(x0)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体P﹣ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= ![]() .
. 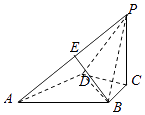
(1)求证:PA⊥BD;
(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于空间两不同的直线![]() ,两不同的平面
,两不同的平面![]() ,有下列推理:
,有下列推理:
(1)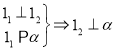 , (2)
, (2)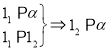 ,(3)
,(3)![]()
(4)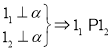 , (5)
, (5)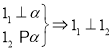
其中推理正确的序号为( )
A. (1)(3)(4) B. (2)(3)(5) C. (4)(5) D. (2)(3)(4)(5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com