
����Ŀ����һ�����͵�ϴ��Һ��ȥ���ٶ��ر��.��֪ÿͶ��![]() ��
��![]() ��
��![]() ������λ��ϴ��Һ��һ����ˮ��ϴ�»��У�����ˮ���ͷŵ�Ũ��
������λ��ϴ��Һ��һ����ˮ��ϴ�»��У�����ˮ���ͷŵ�Ũ��![]() ����/��������ʱ��
����/��������ʱ��![]() (����) �仯�ĺ�����ϵʽ����Ϊ
(����) �仯�ĺ�����ϵʽ����Ϊ![]() ������
������ .���ݾ��飬��ˮ��ϴ��Һ��Ũ�Ȳ�����4(��/����ʱ������������Чȥ�۵�����.
.���ݾ��飬��ˮ��ϴ��Һ��Ũ�Ȳ�����4(��/����ʱ������������Чȥ�۵�����.
��1����Ͷ��![]() ����λ��ϴ��Һ��3����ʱˮ��ϴ��Һ��Ũ��Ϊ4 (��/��������
����λ��ϴ��Һ��3����ʱˮ��ϴ��Һ��Ũ��Ϊ4 (��/��������![]() ��ֵ��
��ֵ��
��2����Ͷ��4����λ��ϴ��Һ������Чȥ��ʱ��ɴX���ӣ�
���𰸡���1��![]() ����2�� 14����.
����2�� 14����.
�������������������1����֪![]() ����ʱϴ��Һ��Ũ��Ϊ
����ʱϴ��Һ��Ũ��Ϊ![]() ��/��������
��/��������![]() ʱ�ĺ�����ϵʽ�ɵ�
ʱ�ĺ�����ϵʽ�ɵ�![]() ,���
,���![]() ���ɵõ�
���ɵõ�![]() ��ֵ��(2)��
��ֵ��(2)��![]() ʱ,��������ɵõ�
ʱ,��������ɵõ�![]() ����
����![]() �ĺ�����ϵʽ���ú�����
�ĺ�����ϵʽ���ú�����![]() ���Σ�Ҫ��Чȥ��,��
���Σ�Ҫ��Чȥ��,��![]() ,���ݺ�����ϵʽ�ֱ����
,���ݺ�����ϵʽ�ֱ����![]() ��������Чȥ��ʱ
��������Чȥ��ʱ![]() �ķ�Χ,�ۺ�����������ɵõ���Чȥ�۵�ʱ��.
�ķ�Χ,�ۺ�����������ɵõ���Чȥ�۵�ʱ��.
�����������1��������֪�� ![]() �� ���
�� ���![]() ��
��
��2����![]() ������
������
��![]() ʱ����
ʱ����![]() ���
���![]() ������
������![]() .
.
��![]() ʱ����
ʱ����![]() ���
���![]() ������
������![]()
���ϣ� ![]() .
.
�𣺹���Ͷ��4����λ��ϴ��Һ������Чȥ��ʱ��ɴ�14����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �������ⳤ��������Ҳ��ⴹֱ�ڵ�������
�������ⳤ��������Ҳ��ⴹֱ�ڵ�������![]() ���������澭����
���������澭����![]() ����
����![]() �����·�߳�Ϊ
�����·�߳�Ϊ![]() �����������·����
�����������·����![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��
��
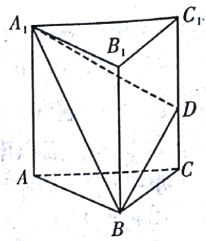
��1����������![]() �������
�������
��2��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c����tanA��tanB= ![]() ��1+tanAtanB���� ������c2=a2+b2��ab�����A��B��C�Ĵ�С��
��1+tanAtanB���� ������c2=a2+b2��ab�����A��B��C�Ĵ�С��
������֪���� ![]() =��sinA��cosA����
=��sinA��cosA���� ![]() =��cosB��sinB������|3
=��cosB��sinB������|3 ![]() ��2
��2 ![]() |��ȡֵ��Χ��
|��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�
�� ![]() ����
����![]() ����
����![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ� ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е�.
���е�.
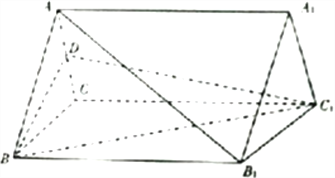
��1����֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=loga ![]() ��a��0��a��1�����溯����
��a��0��a��1�����溯����
��1����ʵ��m��ֵ��
��2���жϺ���f��x�������䣨1��+�ޣ��ϵĵ����Բ�˵�����ɣ�
��3����x�ʣ�n��a��2��ʱ������f��x����ֵ��Ϊ��1��+�ޣ�����ʵ��n��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������жϣ� ��f��x��= ![]() ��g��x��=
��g��x��= ![]() ��ʾͬһ������
��ʾͬһ������
�ں���y=f��x����ͼ����ֱ��x=1�Ľ��������1����
��f��x��=x2��2x+1��g��t��=t2��2t+1��ͬһ������
����f��x��=|x��1|��|x|����f��f�� ![]() ����=0��
����=0��
������ȷ�жϵ������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1����֪f�� ![]() +1��=x+2
+1��=x+2 ![]() ����f��x���Ľ���ʽ��
����f��x���Ľ���ʽ��
��2����֪f��x����һ�κ�����������3f��x+1����2f��x��1��=2x+17����f��x���Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���x3��ax+2=0��������ͬʵ���⣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A.��2��+�ޣ�
B.��3��+�ޣ�
C.��0��3 ��
D.�����ޣ�3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ���Ҵ��ڷ��㳣��
���Ҵ��ڷ��㳣��![]() ��������
��������![]() ��
�� ![]() ����������
����������![]() Ϊ�����ں�����
Ϊ�����ں����� ![]() Ϊ
Ϊ![]() ��������.
��������.
�����������![]() ����
����![]() ����
����![]() ������
������![]() ��ʾ������
��ʾ������![]() ��������������������ں������ǣ�ֱ����д��ţ���
��������������������ں������ǣ�ֱ����д��ţ���
������![]() Ϊ�����ں�������������Ϊ
Ϊ�����ں�������������Ϊ![]() ����֤������
����֤������![]() Ϊ���ں�����
Ϊ���ں�����
������![]() Ϊ�����ں�������
Ϊ�����ں�������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com