
【题目】已知函数![]() 为常数).
为常数).
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,设
时,设![]() 的两个极值点
的两个极值点![]() 恰为
恰为![]() 的零点, 求
的零点, 求![]() 的最小值.
的最小值.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:求单调区间,先求得定义域为![]() ,再求得导数
,再求得导数![]() ,可分
,可分![]() 分别研究
分别研究![]() 的正负,得单调区间;(2)此类问题解决方法是把
的正负,得单调区间;(2)此类问题解决方法是把![]() 表示为
表示为![]() 的函数,因此要想办法把函数式中参数
的函数,因此要想办法把函数式中参数![]() 用
用![]() 表示.首先求得
表示.首先求得![]() ,当
,当![]() 时,
时,![]() ,这样有
,这样有![]() ,再由
,再由![]() ,两式相减得
,两式相减得![]() ,
,
只能求得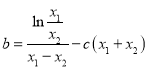 ,而
,而![]() ,代入
,代入![]() 化简为
化简为![]() 的代数式,再利用
的代数式,再利用![]() 得
得![]() ,同除以
,同除以![]() 可得
可得![]() ,这样可由
,这样可由![]() 的范围求得
的范围求得![]() 的取值范围,这样利用导数可得
的取值范围,这样利用导数可得![]() 的最小值.
的最小值.
试题解析:(1)![]() ,
,
当![]() 时,由
时,由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() 单调递增;由
单调递增;由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() ,故
,故![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
![]() 当
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)![]() ,则
,则![]() ,
,![]() 的两根
的两根![]() 即为方程
即为方程
![]() 的两根,
的两根,![]() ,
,![]() ,
,
又![]() 为
为![]() 的零点,
的零点,![]() ,
,
两式相减得![]() ,
,
得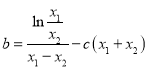 ,而
,而![]() ,
,
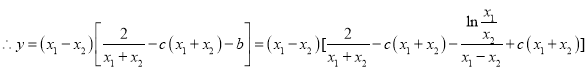
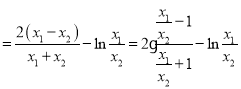 ,令
,令![]() ,由
,由![]() ,得
,得![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() .设
.设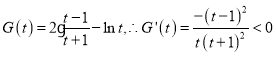 ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,![]() , 即
, 即![]() 的最小值为
的最小值为![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() (单位:万元)和
(单位:万元)和![]() (单位:万元),它们与投入资金
(单位:万元),它们与投入资金![]() (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式![]() ,
,![]() . 今将
. 今将![]() 万元资金投入经营甲、乙两种商品,其中对甲种商品投资
万元资金投入经营甲、乙两种商品,其中对甲种商品投资![]() (单位:万元),
(单位:万元),
(1)试建立总利润![]() (单位:万元)关于
(单位:万元)关于![]() 的函数关系式;
的函数关系式;
(2)当对甲种商品投资![]() (单位:万元)为多少时?总利润
(单位:万元)为多少时?总利润![]() (单位:万元)值最大.
(单位:万元)值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解决某个问题的算法如下:
第一步,给定一个实数n(n≥2).
第二步,判断n是否是2,若n=2,则n满足条件;若n>2,则执行第三步.
第三步,依次从2到n-1检验能不能整除n,若都不能整除n,则n满足条件.
则满足上述条件的实数n是( )
A.质数 B.奇数
C.偶数 D.约数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )和函数
)和函数![]() (
(![]() ,
,![]() ,
,![]() ).问:(1)证明:
).问:(1)证明:![]() 在
在![]() 上是增函数;
上是增函数;
(2)把函数![]() 和
和![]() 写成分段函数的形式,并画出它们的图象,总结出
写成分段函数的形式,并画出它们的图象,总结出![]() 的图象是如何由
的图象是如何由![]() 的图象得到的.请利用上面你的结论说明:
的图象得到的.请利用上面你的结论说明:![]() 的图象关于
的图象关于![]() 对称;
对称;
(3)当![]() ,
,![]() ,
,![]() 时,若
时,若![]() 对于任意的
对于任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
①若直线l与平面α内的一条直线垂直,则l⊥α;
②若直线l与平面α内的两条直线垂直,则l⊥α
③若直线l与平面α内的两条相交直线垂直,则l⊥α;
④若直线l与平面α内的任意一条直线垂直,则l⊥α.
A.4
B.2
C.3
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】梯形ABCD中,AB∥CD,AB平面α,CD平面α,则直线CD与平面α内的直线的位置关系只能是( )
A.平行
B.平行或异面
C.平行或相交
D.异面或相交
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com