练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一个四棱锥P－ABCD的正视图是边长为2的正方形及其一条对角线，侧视图和俯视图全全等的等腰直角三角形，直角边长为2，直观图如图．

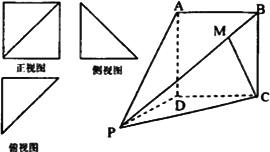
    (1)求四棱锥P－ABCD的体积：

    (2)求直线PC和面PAB所成线面角的余弦值；

    (3)M为棱PB上的一点，当PM长为何值时，CM⊥PA？

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形，且四个顶点都在一个球面上，则该球的表面积为（　　）
    A、
    		2
    πa2
    B、2πa2
    C、
    		3
    πa2
    D、3πa2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在三棱锥P-ABC中，给出下列四个命题：
    ①如果PA⊥BC，PB⊥AC，那么点P在平面ABC内的射影是△ABC的垂心；
    ②如果点P到△ABC的三边所在直线的距离都相等，那么点P在平面ABC内的射影是△ABC的内心；
    ③如果棱PA和BC所成的角为60°，PA=BC=2，E、F分别是棱PB、AC的中点，那么EF=1；
    ④如果三棱锥P-ABC的各条棱长均为1，则该三棱锥在任意一个平面内的射影的面积都不大于
    12
    ．
    其中正确命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：江苏省常州二中2008高考一轮复习综合测试2、数学(文科) 题型：022

    正三棱锥P－ABC的四个顶点同在一个半径为2的球面上，若正三棱锥的侧棱长为2，则正三棱锥的底面边长是________．

    查看答案和解析>>

    科目：高中数学 来源：山东省青岛市2009届高三一模考试(数学理) 题型：044

    在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD为矩形，AB＝PA＝aBC(a＞0)．

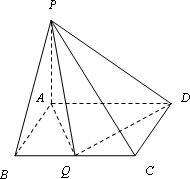
    (Ⅰ)当a＝1时，求证：BD⊥PC；

    (Ⅱ)若BC边上有且只有一个点Q，使得PQ⊥QD，求此时二面角A－PD－Q的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：河北省宣化一中2012届高三新课标高考模拟数学理科试题 题型：044

    在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD为矩形，AB＝PA＝aBC(a＞0)．

    (Ⅰ)当a＝1时，求证：BD⊥PC；

    (Ⅱ)若BC边上有且只有一个点Q，使得PQ⊥QD，求此时二面角A－PD－Q的余弦值．

    查看答案和解析>>

    同步练习册答案