
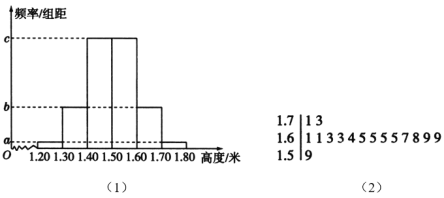
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测100株树苗的高度,经数据处理得到如图(1)所示的频率分布直方图,其中最高的16株树苗的高度的茎叶图如图(2)所示,以这100株树苗的高度的频率估计整批树苗高度的概率.
(1)求这批树苗的高度高于![]() 米的概率,并求图(1)中
米的概率,并求图(1)中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批树苗中随机选取3株,记![]() 为高度在
为高度在![]() 的树苗数量,求
的树苗数量,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批树苗的高度满足近似于正态分布
的概率分布.如果这批树苗的高度满足近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗能否被签收?
的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗能否被签收?
【答案】(1)概率为![]() ,
,![]() ,
,![]() ,
,![]() ;(2)分布列答案见解析,数学期望
;(2)分布列答案见解析,数学期望![]() ;(3)被签收.
;(3)被签收.
【解析】
(1)结合茎叶图,求得每组频率,再求得![]() 的值.
的值.
(2)根据二项分布的知识求得分布列并求得数学期望.
(3)求得![]() 与
与![]() ,由此判断这批树苗的高度满足近似于正态分布
,由此判断这批树苗的高度满足近似于正态分布![]() 的概率分布,应认为这批树苗是合格的,能被签收.
的概率分布,应认为这批树苗是合格的,能被签收.
(1)由题图(2)可知,100株样本树苗中高度高于![]() 米的共有15株,
米的共有15株,
以样本的频率估计总体的概率,可得这批树苗的高度高于![]() 米的概率为
米的概率为![]() .
.
记![]() 为树苗的高度,结合题图(1)(2)可得:
为树苗的高度,结合题图(1)(2)可得:
![]() ,
,
![]() ,
,
![]() .
.
因为组距为![]() ,所以
,所以![]() ,
,![]() ,
,![]() .
.
(2)以样本的频率估计总体的概率,可得:从这批树苗中随机选取1株,高度在![]() 的概率为
的概率为
![]() .
.
因为从这批树苗中随机选取3株,相当于三次独立重复试验,
所以随机变量![]() 服从二项分布
服从二项分布![]() ,
,
故![]() 的分布列为
的分布列为![]() ,
,
即
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() (或
(或![]() ).
).
(3)由![]() ,取
,取![]() ,
,![]() ,
,
由(2)可知,![]() ,
,
又结合(1),可得![]()
![]()
![]() ,
,
所以这批树苗的高度满足近似于正态分布![]() 的概率分布,
的概率分布,
应认为这批树苗是合格的,将顺利被该公司签收.


科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一条线段,且
上的一条线段,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点,则
上的动点,则
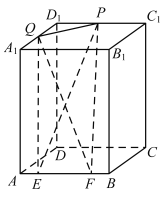
①四面体![]() 的体积为定值
的体积为定值
②直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值
③点![]() 到直线
到直线![]() 的距离为定值
的距离为定值
④直线![]() 与平面
与平面![]() 所成的角为定值
所成的角为定值
其中正确结论的编号是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某试点城市环保局从该市市区2019年上半年每天的
微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某试点城市环保局从该市市区2019年上半年每天的![]() 监测数据中随机的抽取15天的数据作为样本,监测值如下茎叶图所示(十位为茎,个位为叶).
监测数据中随机的抽取15天的数据作为样本,监测值如下茎叶图所示(十位为茎,个位为叶).
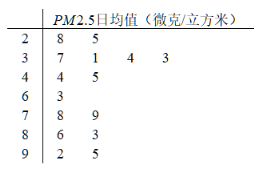
(1)在这15天的![]() 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这15天的数据中任取2天数据,记![]() 表示抽到
表示抽到![]() 监测数据超标的天数,求
监测数据超标的天数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)以这15天的![]() 日均值来估计该市下一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.
日均值来估计该市下一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
科目:高中数学 来源: 题型:
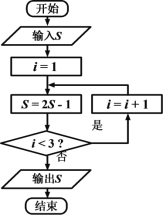
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() 设数列
设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求数列![]() 通项公式;
通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国内疫情形势好转,暂停的中国正在重启,为了尽快提升经济、吸引顾客,哈西某商场举办购物抽奖活动,凡当日购物满1000元的顾客,可参加抽奖,规则如下:盒中有大小质地均相同5个球,其中2个红球和3个白球,不放回地依次摸出2个球,若在第一次和第二次均摸到红球则获得特等奖,否则获得纪念奖,则顾客获得特等奖的概率是_________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以原点为圆心,以短轴长为直径的圆
,且以原点为圆心,以短轴长为直径的圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]()
![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且与圆
,且与圆![]() 没有公共点,设
没有公共点,设![]() 为椭圆
为椭圆![]() 上一点,满足
上一点,满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com