练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，其中表示不超过的最大整数，下列关于说法正确的有:______．

    ①的值域为[-1,1]

    ②为奇函数

    ③为周期函数，且最小正周期T=4

    ④在[0，2）上为单调增函数

    ⑤与的图像有且仅有两个公共点

    【答案】③⑤

    【解析】

    根据已知分析函数f（x）＝sin（[x]）的图象和性质，逐一判断四个结论的真假，可得结论．

    ∵表示不超过的最大整数，

    ∴的值域为{﹣1，0，1}，故①错误；

    ∵函数＝sin（[]）

    ∴ sin（）＝0；

    sin（）＝1．不是奇函数，故②错误；

    作出函数图象，如图所示：

    函数y＝f（x）是周期函数，且最小正周期为4，故③正确；

    在[0，2）上为单调增函数显然错误，故④错误．

    与的图像有且仅有两个公共点，分别是，故⑤正确；

    故真命题为：③⑤，

    故答案为：③⑤．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，直线是曲线的一条切线．

    （1）求实数a的值；

    （2）若对任意的x(0，)，都有，求整数k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒子里装有标号为的张标签，随机的选取两张标签.

    （1）若标签的选取是无放回的，求两张标签上的数字为相邻整数的概率；

    （2）若标签的选取是有放回的，求两张标签上的数字至少有一个为5的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝lnx．

    （1）若a＝4，求函数f（x）的单调区间；

    （2）若函数f（x）在区间（0，1]内单调递增，求实数a的取值范围；

    （3）若x1、x2∈R+，且x1≤x2，求证：（lnx1﹣lnx2）（x1+2x2）≤3（x1﹣x2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市100000名职业中学高三学生参加了一项综合技能测试，从中随机抽取100名学生的测试成绩，制作了以下的测试成绩（满分是184分）的频率分布直方图.

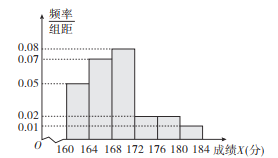
    在频率分布直方图的分组中，以各组的区间中点值代表该组的各个值，测试成绩落入该区间的频率作为测试成绩取该区间中点值的概率.已知甲、乙两名学生的测试成绩分别为168分和170分.

    （1）求技能测试成绩的中位数，对甲、乙的成绩作出客观的评价；

    （2）若市教育局把这次技能测试看作技能大比武，且作出以下奖励规定：

    给测试成绩者颁发奖金元，

    给测试成绩者颁发奖金元，求；

    （3）若市教育局把这次技能看作是毕业过关测试，且作出以下规定：

    当测试成绩时，统一交测试费和补测费300元；

    当测试成绩时，统一交测试费100元；

    当测试成绩时，免交测试费且颁发500元奖金.

    若，据此统计：每个测试者平均最多应该交给教育局多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗 (吨标准煤)的几组对照数据

    （1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

    (附: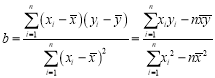，，，，其中,为样本平均值)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业三月中旬生产，，三种产品共3000件，根据分层随机抽样的结果，企业统计员制作了如下的统计表格：

    产品类别

    产品数量

    1300

    样本中的数量

    130

    由于不小心，表格中，产品的有关数据已被污染得看不清楚，统计员只记得样本中产品的数量比样本中产品的数量多10.根据以上信息，求该企业生产产品的数量.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，直线， .

    （1）求证：对，直线与圆总有两个不同的交点；

    （2）求弦的中点的轨迹方程，并说明其轨迹是什么曲线；

    （3）是否存在实数，使得原上有四点到直线的距离为？若存在，求出的范围；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一只口袋有形状大小质地都相同的只小球，这只小球上分别标记着数字.

    甲乙丙三名学生约定：

    （）每个不放回地随机摸取一个球；

    （）按照甲乙丙的次序一次摸取；

    （）谁摸取的球的数字对打，谁就获胜.

    用有序数组表示这个试验的基本事件，例如：表示在一次试验中，甲摸取的是数字，乙摸取的是数字，丙摸取的是数字；表示在一次实验中，甲摸取的是数，乙摸取的是数字，丙摸取的是数字.

    （Ⅰ）列出基本事件，并指出基本事件的总数；

    （Ⅱ）求甲获胜的概率；

    （Ⅲ）写出乙获胜的概率，并指出甲乙丙三名同学获胜的概率与其摸取的次序是否有关？

    查看答案和解析>>

    同步练习册答案