
【题目】已知函数f(x)=lnx![]() .
.
(1)若a=4,求函数f(x)的单调区间;
(2)若函数f(x)在区间(0,1]内单调递增,求实数a的取值范围;
(3)若x1、x2∈R+,且x1≤x2,求证:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)将a=4代入f(x)求出f(x)的导函数,然后根据导函数的符号,得到函数的单调区间;
(2)根据条件将问题转化为![]() 在
在![]() ,
,![]() 上恒成立问题,然后根据函数的单调性求出
上恒成立问题,然后根据函数的单调性求出![]() 的范围;
的范围;
(3)根据条件将问题转化为![]() 成立问题,令
成立问题,令![]() ,即
,即![]() 成立,再利用函数的单调性证明即可.
成立,再利用函数的单调性证明即可.
解:(1)![]() 的定义域是
的定义域是![]() ,
,![]() ,
,
所以![]() 时,
时,![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() ,
,
由![]() ,解得
,解得![]() ,
,
故![]() 在
在![]() 和
和![]() ,
,![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减.
上单调递减.
(2)由(1)得![]() ,
,
若函数![]() 在区间
在区间![]() ,
,![]() 递增,则有
递增,则有![]() 在
在![]() ,
,![]() 上恒成立,
上恒成立,
即![]() 在
在![]() ,
,![]() 上恒成立成立,所以只需
上恒成立成立,所以只需![]() ,
,
因为函数![]() 在
在![]() 时取得最小值9,所以
时取得最小值9,所以![]() ,
,
所以a的取值范围为![]() .
.
(3)当![]() 时,不等式显然成立,
时,不等式显然成立,
当![]() 时,因为
时,因为![]() ,
,![]() ,所以要原不等式成立,
,所以要原不等式成立,
只需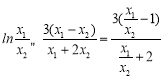 成立即可,
成立即可,
令![]() ,则
,则![]() ,
,
由(2)可知函数![]() 在
在![]() ,
,![]() 递增,所以
递增,所以![]() ,
,
所以![]() 成立,
成立,
所以(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】(用数字作答)从5本不同的故事书和4本不同的数学书中选出4本,送给4位同学,每人1本,问:
(1)如果故事书和数学书各选2本,共有多少种不同的送法?
(2)如果故事书甲和数学书乙必须送出,共有多少种不同的送法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费![]() 元.
元.
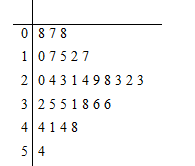
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设![]() 分别为红车,黄车,蓝车的月消费,写出
分别为红车,黄车,蓝车的月消费,写出![]() 与
与![]() 的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌的共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 | (0,15] | (15,30] | (30,45] | (45,60] |
人数 | 16 | 45 | 34 | 5 |
在(2)的活动条件下,每个品牌各应该投放多少辆?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a∈R).
(a∈R).
(Ⅰ)求f(x)在区间[-1,2]上的最值;
(Ⅱ)若过点P(1,4)可作曲线y=f(x)的3条切线,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整;
列联表补充完整;
(2)判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
参考公式: ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,下列关于
的最大整数,下列关于![]() 说法正确的有:______.
说法正确的有:______.
①![]() 的值域为[-1,1]
的值域为[-1,1]
②![]() 为奇函数
为奇函数
③![]() 为周期函数,且最小正周期T=4
为周期函数,且最小正周期T=4
④![]() 在[0,2)上为单调增函数
在[0,2)上为单调增函数
⑤![]() 与
与![]() 的图像有且仅有两个公共点
的图像有且仅有两个公共点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() ,点
,点![]() ,设直线
,设直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() 、
、![]() .
.
(1)若直线![]() 轴,求直线
轴,求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若直线![]() 不垂直于
不垂直于![]() 轴,且
轴,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李根据以往多次考试状态研究得到,今后三次考试数学考![]() 分以上的概率相同.现用随机模拟的方法预测三次考试有两次数学考
分以上的概率相同.现用随机模拟的方法预测三次考试有两次数学考![]() 分以上的概率,规定投一次骰子出现
分以上的概率,规定投一次骰子出现![]() 点和
点和![]() 点代表考
点代表考![]() 分以上;投三次骰子代表三次;产生的三个随机数作为一组.得到的
分以上;投三次骰子代表三次;产生的三个随机数作为一组.得到的![]() 组随机数如下:
组随机数如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .则在此次随机模拟试验中,每次数学考
.则在此次随机模拟试验中,每次数学考![]() 分以上的概率和三次中数学有两次考
分以上的概率和三次中数学有两次考![]() 分以上的概率的近似值分别为( )
分以上的概率的近似值分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com