练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某企业三月中旬生产，，三种产品共3000件，根据分层随机抽样的结果，企业统计员制作了如下的统计表格：

    产品类别

    产品数量

    1300

    样本中的数量

    130

    由于不小心，表格中，产品的有关数据已被污染得看不清楚，统计员只记得样本中产品的数量比样本中产品的数量多10.根据以上信息，求该企业生产产品的数量.

    【答案】800.

    【解析】

    根据每个个体被抽到的频率相等，先求出总体的样本容量，据B产品的样本数得到A、C产品的样本数，再根据A产品的样本容量比C产品的样本容量多10，可得C产品的样本容量，用C产品的样本容量除以每个个体被抽到的频率，可得C产品的数量．

    设样本量为，

    则，

    ，

    在样本中产品和产品共有（件）.

    设样本中产品数量为，则，

    ，

    该企业生产产品的数量为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

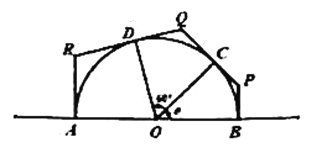
    【题目】为美化城市环境，相关部门需对一半圆形中心广场进行改造出新，为保障市民安全，施工队对广场进行围挡施工．如图，围挡经过直径的两端点A，B及圆周上两点C，D围成一个多边形ABPQR，其中AR，RQ，QP，PB分别与半圆相切于点A，D，C，B．已知该半圆半径OA长30米，∠COD为60°，设∠BOC为．

    （1）求围挡内部四边形OCQD的面积；

    （2）为减少对市民出行的影响，围挡部分面积要尽可能小．求该围挡内部多边形ABPQR面积的最小值？并写出此时的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= （a∈R）.

    （Ⅰ）求f（x）在区间[-1,2]上的最值；

    （Ⅱ）若过点P（1,4）可作曲线y=f（x）的3条切线，求实数a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中表示不超过的最大整数，下列关于说法正确的有:______．

    ①的值域为[-1,1]

    ②为奇函数

    ③为周期函数，且最小正周期T=4

    ④在[0，2）上为单调增函数

    ⑤与的图像有且仅有两个公共点

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=1-（a＞0且a≠1）是定义在（-∞，+∞）上的奇函数．

    （1）求a的值；

    （2）证明：函数f（x）在定义域（-∞，+∞）内是增函数；

    （3）当x∈（0，1]时，tf（x）≥2x-2恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，抛物线，点，设直线与交于不同的两点、.

    （1）若直线轴，求直线的斜率的取值范围；

    （2）若直线不垂直于轴，且，证明：直线过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线被圆截得的弦长为.

    (1)求的值；

    (2)求过点并与圆C相切的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用红、黄、蓝三种不同的颜色给大小相同的三个圆随机涂色，每个圆只涂一种颜色.设事件“三个圆的颜色全不相同”，事件“三个圆的颜色不全相同”，事件“其中两个圆的颜色相同”，事件“三个圆的颜色全相同”.

    （1）写出试验的样本空间.

    （2）用集合的形式表示事件.

    （3）事件与事件有什么关系？事件和的交事件与事件有什么关系？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象关于原点对称，其中为常数.

    （1）求的值；

    （2）当时， 恒成立，求实数的取值范围；

    （3）若关于的方程在上有解，求的取值范围.

    查看答案和解析>>

    同步练习册答案