
【题目】某公司为加强对销售员的考核与管理,从销售部门随机抽取了2019年度某一销售小组的月均销售额,该小组各组员2019年度的月均销售额(单位:万元)分别为:3.35,3.35,3.38,3.41,3.43,3.44,3.46,3.48,3.51,3.54,3.56,3.56,3.57,3.59,3.60,3.64,3.64,3.67,3.70,3.70.
(Ⅰ)根据公司人力资源部门的要求,若月均销售额超过3.52万元的组员不低于全组人数的![]() ,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
(Ⅱ)在该销售小组中,已知月均销售额最高的5名销售员中有1名的月均销售额造假.为找出月均销售额造假的组员,现决定请专业机构对这5名销售员的月均销售额逐一进行审核,直到能确定出造假组员为止.设审核次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(Ⅰ)不需要对该销售小组发放奖励;(Ⅱ)分布列见解析,![]() .
.
【解析】
(Ⅰ)根据该小组![]() 名销售员中有11名销售员2019年度月均销售额超过3.52万元可知,月均销售额超过3.52万元的销售员占该小组的比例为
名销售员中有11名销售员2019年度月均销售额超过3.52万元可知,月均销售额超过3.52万元的销售员占该小组的比例为![]() ,低于
,低于![]() ,即可判断不需要对该销售小组发放奖励;
,即可判断不需要对该销售小组发放奖励;
(Ⅱ)由题意知随机变量![]() 的可能取值为1,2,3,4,
的可能取值为1,2,3,4,![]() ,
,![]() ,即可写出分布列,求出数学期望.
,即可写出分布列,求出数学期望.
(Ⅰ)该小组共有11名销售员2019年度月均销售额超过3.52万元,分别是:3.54,3.56,3.56,3.57,3.59,3.60,3.64,3.64,3.67,3.70,3.70.
∴月均销售额超过3.52万元的销售员占该小组的比例为![]() .
.
∵![]() ,故不需要对该销售小组发放奖励.
,故不需要对该销售小组发放奖励.
(Ⅱ)由题意,随机变量![]() 的可能取值为1,2,3,4.
的可能取值为1,2,3,4.
则![]() ,
,![]() ,
,![]() ,
,
![]() .
.
∴随机变量![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,点
,点![]() 是
是![]() 上的不同于顶点的动点,
上的不同于顶点的动点,![]() 上在点
上在点![]() 处的切线
处的切线![]() 分别与
分别与![]() 轴轴交于点
轴轴交于点![]() 、
、![]() .若存在常数
.若存在常数![]() 满足对任意的点
满足对任意的点![]() 都有
都有![]() .
.
(Ⅰ)求实数![]() ,
,![]() 的值;
的值;
(Ⅱ)过点![]() 作
作![]() 的垂线与
的垂线与![]() 交于不同于
交于不同于![]() 的一点
的一点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρsin2θ-8cosθ=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.在直角坐标系中,倾斜角为α的直线l过点P(2,0).
(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设点Q与点G的极坐标分别为![]() ,(2,π),若直线l经过点Q
,(2,π),若直线l经过点Q![]() ,且与曲线C相交于A,B两点,求△GAB的面积.
,且与曲线C相交于A,B两点,求△GAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校两个班级100名学生在一次考试中的成绩的频率分布直方图如图所示,其中成绩分组区如下表:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
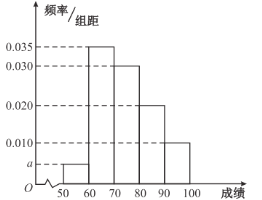
(1)求频率表分布直方图中a的值;
(2)根据频率表分布直方图,估计这100名学生这次考试成绩的平均分;
(3)现用分层抽样的方法从第三、四、五组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
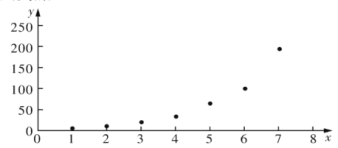
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: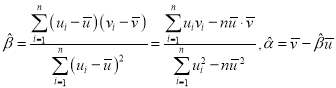 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的发展与进步,传播和存储状态已全面进入数字时代,以数字格式存储,以互联网为平台进行传输的音乐——数字音乐已然融入了我们的日常生活.虽然我国音乐相关市场仍处在起步阶段,但政策利好使音乐产业逐渐得到资本市场更多的关注.对比如下两幅统计图,下列说法正确的是( )
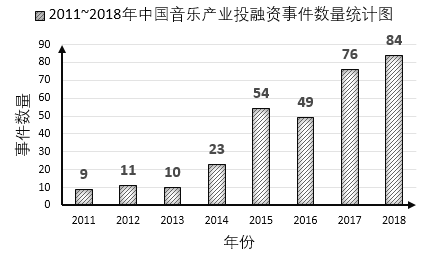
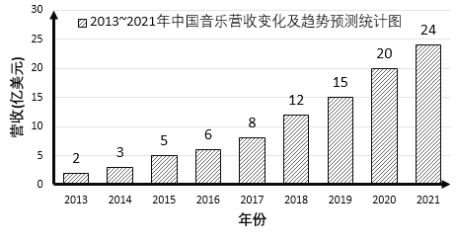
A.2011~2018年我国音乐产业投融资事件数量逐年增长
B.2013~2018年我国录制音乐营收与音乐产业投融资事件数量呈正相关关系
C.2016年我国音乐产业投融资事件的平均营收约为1.27亿美元
D.2013~2019年我国录制音乐营收年增长率最大的是2018年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 绕极点逆时针旋转
绕极点逆时针旋转![]() 后得到曲线
后得到曲线![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() :
:![]() 与
与![]() ,
,![]() 分别相交于异于极点的
分别相交于异于极点的![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
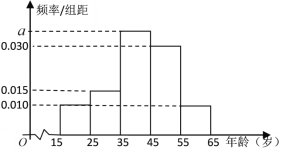
(1)求![]() 的值;
的值;
(2)求出样本的平均数(同一组数据用该区间的中点值作代表);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求第2组中抽到
人进行问卷调查,求第2组中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com