
【题目】已知一列函数![]() ,设直线
,设直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的最小值,并指出此时
的最小值,并指出此时![]() 的取值;
的取值;
(2)在![]() 中任取一个函数,求该函数在
中任取一个函数,求该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率;
上是减函数的概率;
(3)是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)不存在
(3)不存在
【解析】
(1)根据题意表示出![]() ,结合基本不等式即可求得最小值及取得最小值时
,结合基本不等式即可求得最小值及取得最小值时![]() 的值.
的值.
(2)根据函数表达式,结合打勾函数的图像与性质,即可判断在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的所有情况,即可求得在
上是减函数的所有情况,即可求得在![]() 中满足条件的概率.
中满足条件的概率.
(3)由直线![]() 与
与![]() 的交点为
的交点为![]() ,即可求得点
,即可求得点![]() 的坐标.由点
的坐标.由点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,结合点到直线距离公式即可求得
,结合点到直线距离公式即可求得![]() 的坐标.表示出
的坐标.表示出![]() 的面积
的面积![]() ,
,![]() 的面积
的面积![]() .将、
.将、![]() 的表达式代入等式
的表达式代入等式![]() 中,通过化简变形,检验即可得知
中,通过化简变形,检验即可得知![]() 的值,若不存在.
的值,若不存在.
(1)函数![]()
所以![]()
由基本不等式可知, ![]()
当且仅当![]() 时取等号,即
时取等号,即![]() 时取等号
时取等号
所以![]() 的最小值为
的最小值为![]() ,当
,当![]() 时取等号
时取等号
(2)因为![]() 结合对勾函数的图像与性质
结合对勾函数的图像与性质
所以![]()
![]()
![]()
![]()
在![]() 内满足单调递增,而
内满足单调递增,而![]() 不满足.因而满足在
不满足.因而满足在![]() 内满足单调递增的函数共有49个.
内满足单调递增的函数共有49个.
因为![]() ,而
,而![]()
而![]()
![]()
![]() 满足在
满足在![]() 内单调递减,所以此时共有
内单调递减,所以此时共有![]()
所以该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的个数共有
上是减函数的个数共有![]() 个
个
即该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率为
上是减函数的概率为![]()
(3)因为直线![]() 与
与![]() 的交点为
的交点为![]()
所以![]()
点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,所以
,所以![]()
点![]() 在直线
在直线![]() 上的射影为
上的射影为![]() ,直线方程化为一般式可得
,直线方程化为一般式可得![]()
则由点到直线距离公式可得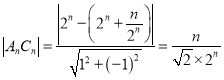
从![]() 向
向![]() 轴作垂直,交
轴作垂直,交![]() 于点E
于点E
则![]()
所以![]()
![]()
画出函数图像如下图所示:
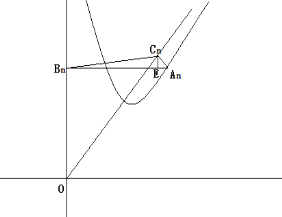
所以![]() 的面积为
的面积为![]()
![]() 的面积为
的面积为![]()
![]()
假设存在正整数![]() ,使得
,使得![]() 成立,代入可得
成立,代入可得
![]()
将式子化简可得![]()
当![]() 时,等式左边等于20,等式右边等于17,等式不成立
时,等式左边等于20,等式右边等于17,等式不成立
当![]() 时,等式左边等于32,等式右边等于68,等式不成立
时,等式左边等于32,等式右边等于68,等式不成立
当![]() 时,等式左边小于0,等式右边大于0,等式不成立.
时,等式左边小于0,等式右边大于0,等式不成立.
综上可知,不存在正整数![]() ,使得
,使得![]() 成立
成立


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某市计划在一片空地上建一个集购物、餐饮、娱乐为一体的大型综合园区,如图,已知两个购物广场的占地都呈正方形,它们的面积分别为13公顷和8公顷;美食城和欢乐大世界的占地也都呈正方形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为
公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷.
公顷.
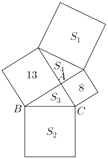
(1)设![]() ,用关于
,用关于![]() 的函数
的函数![]() 表示
表示![]() ,并求
,并求![]() 在区间
在区间![]() 上的最大值的近似值(精确到0.001公顷);
上的最大值的近似值(精确到0.001公顷);
(2)如果![]() ,并且
,并且![]() ,试分别求出
,试分别求出![]() 、
、![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是以d为公差的等差数列,{bn}数列是以q为公比的等比数列.
(1)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3<a1003+5b2﹣2010,求整数q的值;
(2)在(1)的条件下,试问数列中是否存在一项bk,使得bk恰好可以表示为该数列中连续p(p∈N,p≥2)项的和?请说明理由;
(3)若b1=ar,b2=as≠ar,b3=at(其中t>s>r,且(s﹣r)是(t﹣r)的约数),求证:数列{bn}中每一项都是数列{an}中的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,对坐标平面上任意一点
,对坐标平面上任意一点![]() ,定义
,定义![]() ,若两点
,若两点![]() ,
,![]() ,满足
,满足![]() ,称点
,称点![]() ,
,![]() 在曲线
在曲线![]() 同侧;
同侧;![]() ,称点
,称点![]() ,
,![]() 在曲线
在曲线![]() 两侧.
两侧.
(1)直线![]() 过原点,线段
过原点,线段![]() 上所有点都在直线
上所有点都在直线![]() 同侧,其中
同侧,其中![]() ,
,![]() ,求直线
,求直线![]() 的倾斜角的取值范围;
的倾斜角的取值范围;
(2)已知曲线![]() ,
,![]() 为坐标原点,求点集
为坐标原点,求点集![]() 的面积;
的面积;
(3)记到点![]() 与到
与到![]() 轴距离和为
轴距离和为![]() 的点的轨迹为曲线
的点的轨迹为曲线![]() ,曲线
,曲线![]() ,若曲线
,若曲线![]() 上总存在两点
上总存在两点![]() ,
,![]() 在曲线
在曲线![]() 两侧,求曲线
两侧,求曲线![]() 的方程与实数
的方程与实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减,②存在常数
上单调递减,②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“渐近函数”,说明理由;
的“渐近函数”,说明理由;
(2)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)若函数![]() ,
,![]() ,求证:当且仅当
,求证:当且仅当![]() 时,
时,![]() 是
是![]() 的“渐近函数”.
的“渐近函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项不为0,前
各项不为0,前![]() 项和为
项和为![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的条件下,已知![]() ,分别求
,分别求![]() 和
和![]() 的表达式;
的表达式;
(3)证明:![]() 是等差数列的充要条件是:对任意
是等差数列的充要条件是:对任意![]() ,都有:
,都有:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com