
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以直角坐标系的原点
为参数),在以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高生产效益,某企业引进了一批新的生产设备,为了解设备生产产品的质量情况,分别从新、旧设备所生产的产品中,各随机抽取100件产品进行质量检测,所有产品质量指标值均在![]() 以内,规定质量指标值大于30的产品为优质品,质量指标值在
以内,规定质量指标值大于30的产品为优质品,质量指标值在![]() 的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
质量指标值 | 频数 |
| 2 |
| 8 |
| 20 |
| 30 |
| 25 |
| 15 |
合计 | 100 |
(1)请分别估计新、旧设备所生产的产品的优质品率.
(2)优质品率是衡量一台设备性能高低的重要指标,优质品率越高说明设备的性能越高,根据已知图表数据填写下面列联表(单位:件),并判断是否有![]() 的把握认为“产品质量高于新设备有关”.
的把握认为“产品质量高于新设备有关”.
非优质品 | 优质品 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
附:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
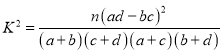 ,其中
,其中![]() .
.
(3)已知每件产品的纯利润y(单位:元)与产品质量指标值t的关系式为![]() 若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代教育要求学生掌握“六艺”,即“礼、乐、射、御、书、数”.某校为弘扬中国传统文化,举行有关“六艺”的知识竞赛.甲、乙、丙三位同学进行了决赛.决赛规则:决赛共分![]() 场,每场比赛的第一名、第二名、第三名的得分分别为
场,每场比赛的第一名、第二名、第三名的得分分别为![]() ,选手最后得分为各场得分之和,决赛结果是甲最后得分为
,选手最后得分为各场得分之和,决赛结果是甲最后得分为![]() 分,乙和丙最后得分都为
分,乙和丙最后得分都为![]() 分,且乙在其中一场比赛中获得第一名,现有下列说法:
分,且乙在其中一场比赛中获得第一名,现有下列说法:
①每场比赛第一名得分![]() 分;
分;
②甲可能有一场比赛获得第二名;
③乙有四场比赛获得第三名;
④丙可能有一场比赛获得第一名.
则以上说法中正确的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com