
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
【答案】(1)x2+(y﹣1)2=1(y≠0).(2)![]() .
.
【解析】
(1)设出![]() 的极坐标,然后由题意得出极坐标方程,最后转化为直角坐标方程为
的极坐标,然后由题意得出极坐标方程,最后转化为直角坐标方程为![]() ;
;
(2)利用(1)中的结论,设出点的极坐标,然后结合面积公式得到面积的三角函数,结合三角函数的性质可得![]() 面积的最大值为
面积的最大值为![]() .
.
解:(1)设P的极坐标为(ρ,θ)(ρ>0),M的极坐标为(ρ0,θ)(ρ0>0).
由题设知|PO|=ρ,![]() .
.
由![]() 4,
4,
得![]() ,
,
所以C2的极坐标方程ρ=2sinθ(ρ>0),
因此C2的直角坐标方程为x2+(y﹣1)2=1(y≠0).
(2)依题意:![]() ,|OB|=ρ2=2sinα.
,|OB|=ρ2=2sinα.
于是△OAB面积:S![]() .
.
当![]() 时,S取得最大值
时,S取得最大值![]() .
.
所以△OAB面积的最大值为![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2+pn,且a4,a7,a12成等比数列.
(1)求数列{an}的通项公式;
(2)若bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(3)判断数列![]() 中是否存在三项成等差数列,并证明你的结论.
中是否存在三项成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办的体育节设有投篮项目.该项目规定:每位同学仅有三次投篮机会,其中前两次投篮每投中一次得1分,第三次投篮投中得2分,若不中不得分,投完三次后累计总分.
(1)若甲同学每次投篮命中的概率为![]() ,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
(2)若(1)中的甲同学邀请乙同学一起参加投篮项目,已知乙同学每次投篮命中的概率为![]() ,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
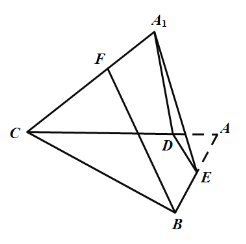
【题目】如图,在边长为4的正三角形![]() 中,E为边
中,E为边![]() 的中点,过E作
的中点,过E作![]() 于D.把
于D.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,连结
的位置,连结![]() .翻折过程中,其中正确的结论是( )
.翻折过程中,其中正确的结论是( )
A.![]() ;
;
B.存在某个位置,使![]() ;
;
C.若![]() ,则
,则![]() 的长是定值;
的长是定值;
D.若![]() ,则四面体
,则四面体![]() 的体积最大值为
的体积最大值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com